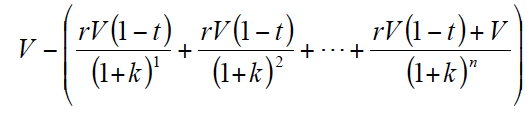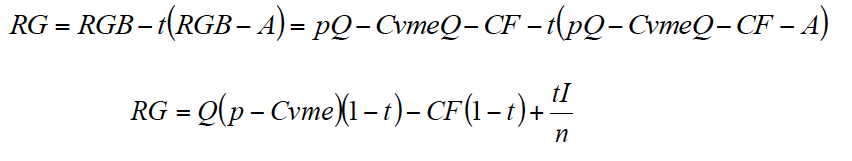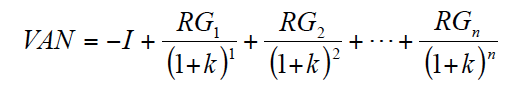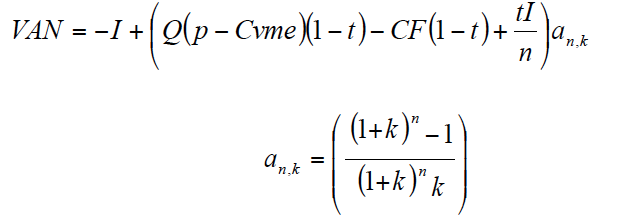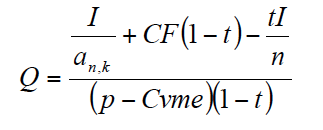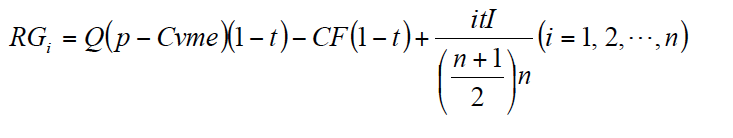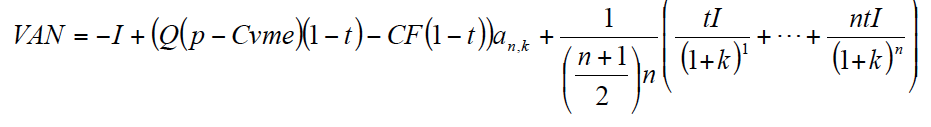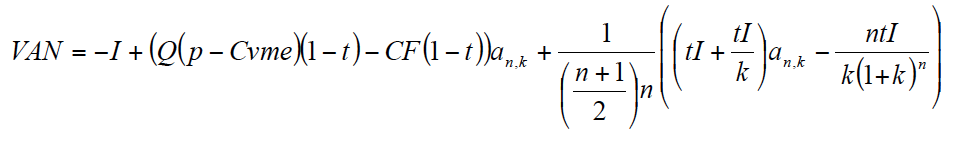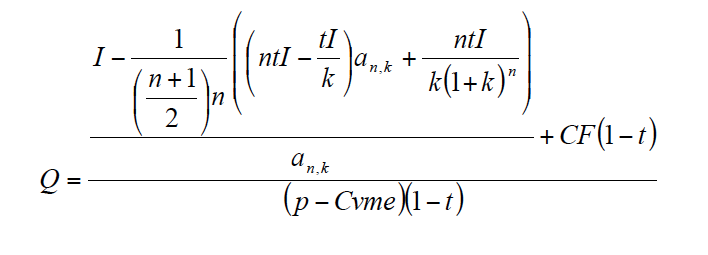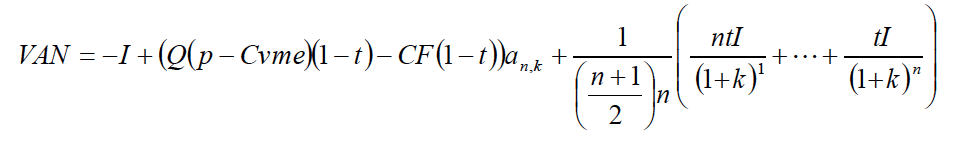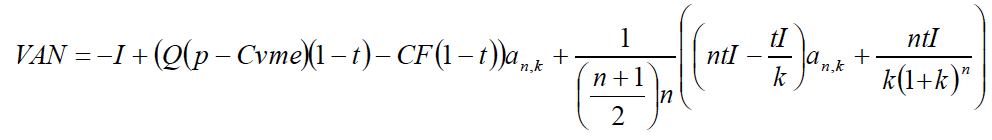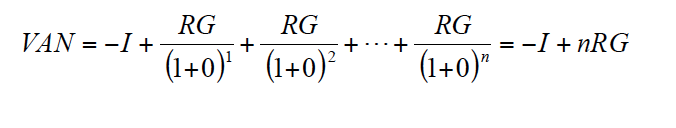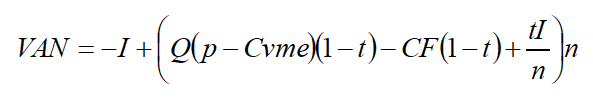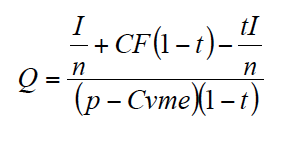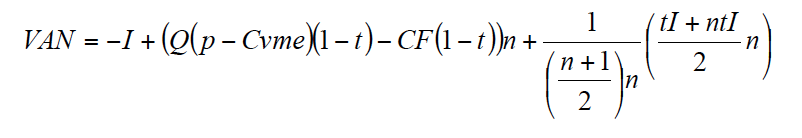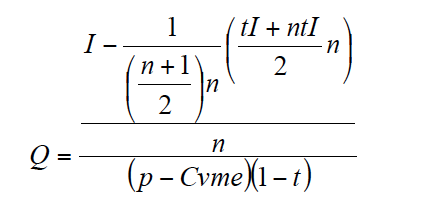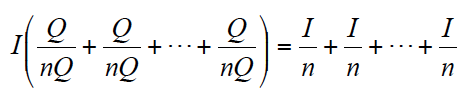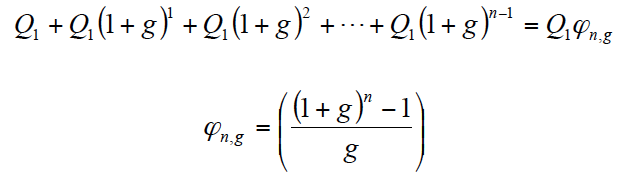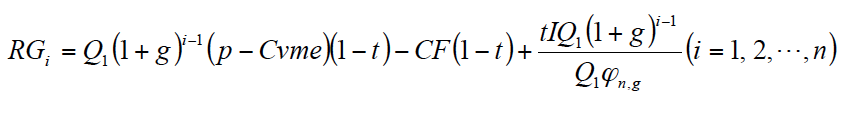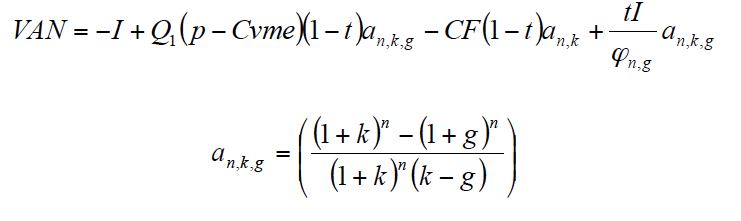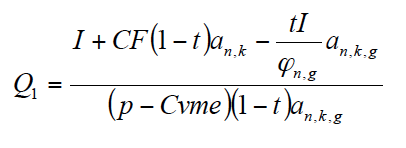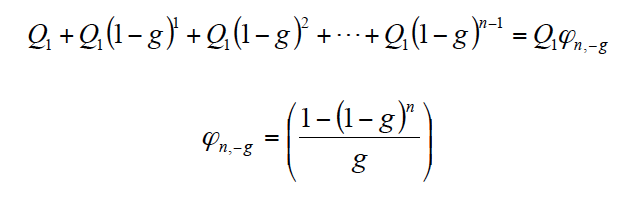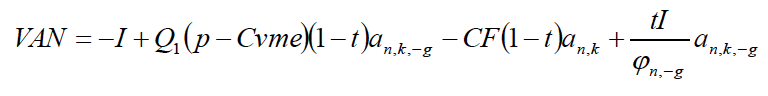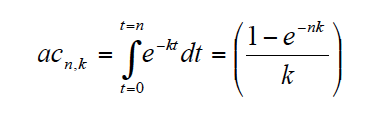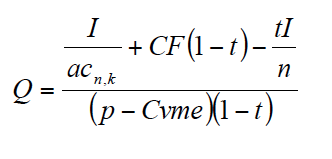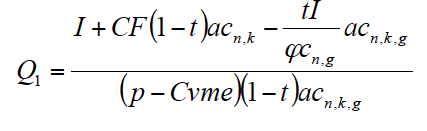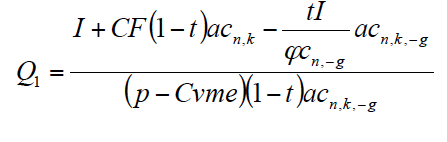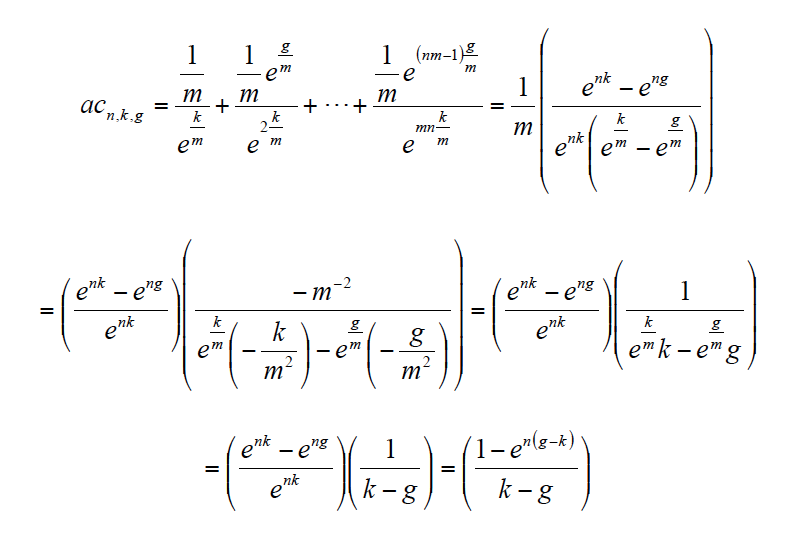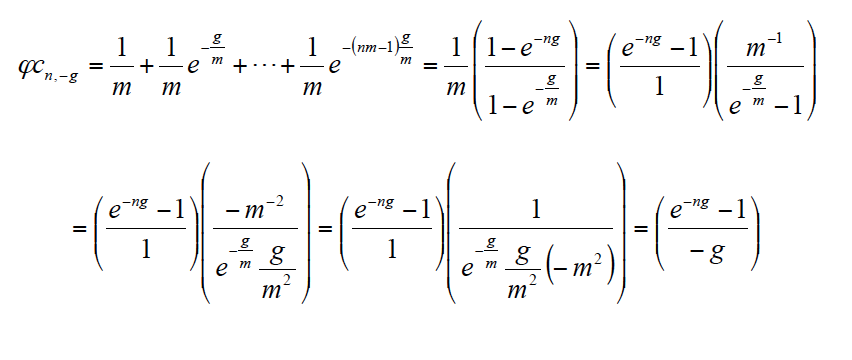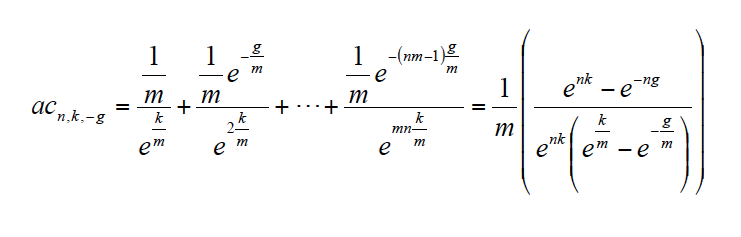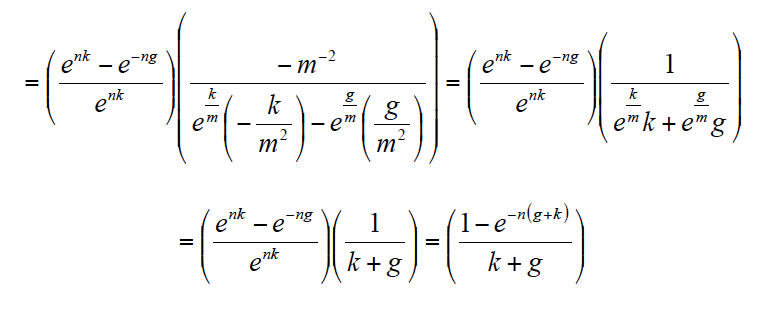Sensibilidad del VAN en relación a la cantidad de producto anual según tipo de amortización
1. INTRODUCCIÓN
Las decisiones de inversión pueden realizarse bajo tres condiciones distintas en función del grado de conocimiento que tengamos sobre los estados de la naturaleza: a) decisiones en condiciones de certeza (sabemos con toda seguridad el estado de la naturaleza que se va a presentar), b) decisiones en condiciones de incertidumbre, (no sabemos nada acerca de los estados de la naturaleza que se pueden presentar), c) decisiones de condiciones de riesgo (tenemos un conocimiento parcial sobre los estados de la naturaleza que van aparecer, pudiéndose asignar probabilidades a cada uno de ellos), (Suárez, 2005, Alegre et al., 2006). Lo anterior, aplicado al criterio de selección de inversiones VAN, implica que en el primer caso se conocen las variables que definen la inversión con probabilidad igual a uno, en el segundo se desconocen dichas probabilidades, mientras que en el tercero podemos asignar probabilidades a cada variable.
Siguiendo a Suárez (2005), existen varios enfoques para tratar las decisiones de inversión en condiciones de riesgo utilizando el criterio VAN. Algunos de estos enfoques van desde la construcción de una distribución de probabilidades hasta la asunción de una distribución concreta como la triangular, la rectangular o la normal, lo que nos permite inferir resultados en términos de probabilidad. Prosiguiendo con dicho autor y otros (Montllor, 1986, Brealey et al., 2014), otra forma de inferir el riesgo en las decisiones de inversión es mediante la inclusión del análisis de sensibilidad, según el cual, admitimos variabilidad en una de las variables manteniendo el resto constantes (clausula ceteris-paribus). La variable sujeta a variabilidad, es aquella que no podemos cuantificar con exactitud o es la que muestra mayor dificultad en su concreción. En el VAN, puede ser cualquiera de sus variables. En nuestro caso concreto será la cantidad de producto anual necesaria para anular el VAN.
El interés sobre la cantidad de producto ha sido puesto de manifiesto por Tarzia (2007), desarrollando un modelo que obtiene una expresión explicita del VAN en función de la cantidad de producto anual. A continuación estudia la sensibilidad del VAN en relación a dicha cantidad y la sensibilidad de esta última respecto de la tasa de descuento. Finalmente relaciona la cantidad de producto con el punto de equilibrio contable. También Nassir (2004) muestra interés por esta variable, ya que si al analizar una inversión observamos que la cantidad de producto es muy sensible, puede hacer desaconsejable su realización. Rescatamos esta idea en el ejemplo que sobre las inversiones A y B, presentamos en la tabla 1:
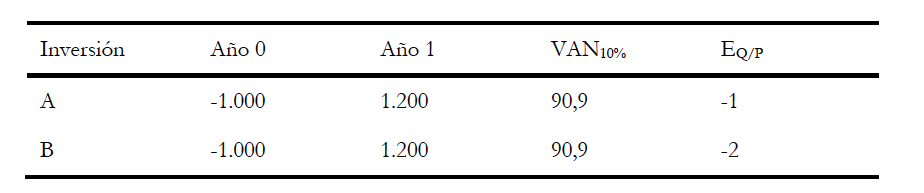
Tabla 1. Flujos de caja, VAN y EQ/P
Fuente: Elaboración propia.
Las inversiones A y B presentan el mismo valor en todos los parámetros excepto en la elasticidad de la cantidad respecto del precio, EQ/P. Ahora bien, mientras que el flujo de caja del año 1 de A consta de 120 unidades de producto a un precio de 10, el flujo de caja de B consta de 20 unidades a un precio de 60. Si suponemos que el precio del producto aumenta en un 10%, el efecto sobre la cantidad es muy distinto en A que en B. En la inversión A la nueva cantidad es 108 mientras que en la inversión B es 16. Esto supondría un VAN de 80 en A y un VAN de -40 en B. La sensibilidad de la cantidad ante variaciones del precio justificaría rechazar la inversión B. En este caso hemos introducido el componente riesgo en las decisiones de inversión sin incluir probabilidades.
Conocer la cantidad de producto anual que anula el VAN es el objetivo principal de este trabajo. En este sentido, desarrollamos un modelo bajo dos supuestos. En el primero, utilizamos el criterio tradicional de la amortización según el cual, ésta se calcula en función del precio de adquisición del equipo productivo y de su vida útil. El cálculo se extiende a tres métodos de amortización (amortización constante, dígitos crecientes y dígitos decrecientes), obteniéndose tres modelos distintos que posteriormente relacionaremos con el punto de equilibrio contable. En este caso suponemos que la amortización es independiente de la cantidad de producto, tratándose de un coste fijo. En el segundo supuesto, la amortización depende de la cantidad de producto anual y de la capacidad del equipo productivo a lo largo de su vida útil, teniendo en cuenta que dicha cantidad puede ser constante o variable, creciente o decreciente según determinada ley geométrica[1]. Extenderemos el modelo al caso de continuidad en la producción. En ambos supuestos, los modelos son examinados con dos tipos de financiación (propia y ajena). La financiación propia se concreta con una emisión de acciones y la financiación ajena con un préstamo. En cada caso el modelo es sometido a un pequeño ejercicio de simulación, comparándose los resultados obtenidos. El modelo así obtenido es genérico y tiene preferentemente carácter divulgativo, especialmente adecuado para su utilización docente[2].
2. MODELO A DESARROLLAR: CONCEPTOS GENERALES
Definimos las variables del modelo: 1) cantidad de producto anual Q (variable principal del problema que sometemos a variabilidad), 2) precio del producto p, 3) coste variable medio Cvme, 4) coste fijo anual CF, (excluida la amortización), 5) amortización anual del equipo productivo A (independiente de la cantidad de producto), 6) tasa de dividendo o de interés sobre la financiación r, 7) tasa impositiva sobre beneficios t, 8) coste anual de la financiación k, 9) duración de la inversión n. Además, partimos de los siguientes supuestos adicionales: a) importe de la inversión I igual al importe de la financiación V, b) inversión, financiación y vida útil del equipo productivo tienen la misma duración, c) valor residual del equipo productivo nulo, d) ausencia de gastos de formalización, primas de emisión y primas de amortización en la financiación.
El recurso generado por la inversión RG es calculado a partir de las magnitudes y variables anuales que son presentadas en la tabla 2:
Tabla 2. Magnitudes y variables relevantes
| Ingresos | IN | p×Q |
| (Costes variables) | (CV) | (Cvme×Q) |
| Margen bruto comercial | MBC | (p-cvme)Q |
| (Costes fijos) | (CF) | (CF) |
| Recursos generados brutos | RGB | MBC - CF |
| (Amortización) | (A) | (A) |
| Beneficio antes de intereses e impuestos | BAII | RGB - A |
| Recurso generado | RG | RGB - t×BAII |
Fuente: Elaboración propia.
A partir de aquí, definimos el recurso generado por la inversión como el flujo de caja después de impuestos y antes de toda financiación, es decir: RG = RGB - t(RGB - A)[3]. Por consiguiente, el concepto de recurso generado implica que el ahorro impositivo de los intereses se recoge en el proyecto de financiación. A continuación, analizamos brevemente el proyecto de financiación.
2.1. PROYECTO DE FINANCIACIÓN
Partimos del supuesto de un proyecto de financiación simple; es decir, aquel en el que al inicio se recibe el importe de la financiación, desembolsándose posteriormente los importes correspondientes a dividendos, intereses y amortización[4]. Si además se cumple que el valor de la suma de las cantidades desembolsadas es mayor que el importe recibido aseguramos la existencia de una sola TIR > 0 (coste de capital en este caso). Es lo que tradicionalmente viene denominándose como un proyecto de financiación puro, ya que sus saldos evaluados a la TIR (coste de capital) son positivos cada año excepto en el último, que es nulo[5]. Sea la siguiente financiación con vencimiento único:
Para valores conocidos de V, r, n y t e igualando a cero la expresión anterior, obtenemos el coste de capital anual, k. Con financiación propia, (no existe ahorro impositivo y t = 0), la resolución de la expresión muestra que r = k; mientras que con financiación ajena, (existe ahorro impositivo y t > 0), muestra que k = r(1-t). Esta disminución del coste de capital con financiación ajena es consecuencia del carácter deducible de los intereses a efectos impositivos, hecho que no se cumple con los dividendos. Como señalamos anteriormente, el que podamos establecer que k = r y que k = r(1-t), es indiferente al método de amortización utilizado en la financiación, siempre que no existan gastos de formalización o colocación a cargo de la empresa, ni primas de emisión, ni primas de amortización. Por consiguiente, los recursos generados anuales que aparecen posteriormente en el cálculo del VAN no recogen el ahorro impositivo de los intereses, el cual ya ha sido recogido en el correspondiente proyecto de financiación.
2.2. CONCEPTO DE AMORTIZACIÓN
Como es sabido, el término amortización aplicado sobre el equipo productivo contiene tres significados: técnico, económico y financiero (Cañibano, 1996, Sánchez, 2008, Calleja, 2008). El significado técnico recoge la pérdida de valor irreversible que los equipos productivos tienen a lo largo del tiempo. Esta pérdida viene motivada por el uso al que está sometido el equipo productivo o también por la menor competitividad como consecuencia de la aparición de nuevos avances tecnológicos (obsolescencia). Lo más razonable es que la pérdida de valor venga motivada por ambas causas. El significado económico recoge la imputación de esta pérdida al coste de producción anual. Por último, el significado financiero recoge la conversión de la pérdida anterior en dinero al repercutir el coste de producción al cliente y recuperarlo mediante el cobro de la venta. Por lo tanto, como la amortización se incorpora al coste de producción anual pero no implica pago, formará parte de los recursos generados anuales obtenidos por la empresa. De esta forma, mediante el proceso de la amortización, recuperamos año tras año el importe de la inversión realizada. Finalizado este proceso, la empresa dispondrá de los recursos financieros suficientes para adquirir un nuevo equipo productivo (previa amortización y renovación de la financiación) o para devolver la financiación en el caso de que la actividad de la empresa se extinga, como podría ser el caso de una inversión sujeta a una concesión no renovable[6].
3. CANTIDAD DE PRODUCTO QUE ANULA EL VAN
En este apartado desarrollamos el modelo que determina la cantidad de producto anual que anula el VAN, según tres métodos de amortización. Como en el modelo incide el método de amortización, el tipo impositivo sobre el beneficio empresarial y el carácter deducible de los intereses de la deuda, realizamos una referencia a la normativa fiscal vigente en relación a estas tres cuestiones. Cada una de ellas viene regulada en la Ley del 27 del 2014, (BOE, 2014). En esta ley se realiza una simplificación de las tablas de amortización, apostando por una continuidad en los criterios anteriores, prevaleciendo con carácter general el método lineal, pero admitiendo también los métodos variables como el de números dígitos crecientes y decrecientes, así como el de porcentaje constante sobre base variable para determinados activos. También podrán adaptarse criterios de amortización libre en ciertas clases de empresas como las sociedades anónimas laborales y las sociedades limitadas laborales en determinadas condiciones. En relación al tipo impositivo la ley muestra la tendencia hacia una simplificación del tipo de gravamen, eliminando desgravaciones fiscales que en nuestro país han venido alejando los tipos nominales de los efectivos. De esta manera se apuesta definitivamente por una consonancia con los tipos impositivos europeos y poder hacer realidad la tan deseada convergencia en materia impositiva. En este sentido la Ley mantiene un tipo general del 25%, aunque teniendo en cuenta el objetivo europeo de gravamen único del 20%. En tercer lugar hacemos referencia al carácter deducible de los intereses de la deuda. Esto implica que para tipos nominales iguales, el tipo efectivo de la financiación ajena es sensiblemente inferior al de la financiación propia. Desde esta perspectiva, con el fin de limitar el déficit público en nuestro país, se han introducido algunas normas tendentes a limitar la deducibilidad de los intereses y a potenciar la autofinanciación empresarial. En primer lugar, limitando dicha deducibilidad al 30% del beneficio operativo y también a determinadas operaciones entre las empresas del grupo. En segundo lugar, creando una reserva de nivelación que nos permita reducir la base imponible hasta un 10% de su importe. En esta aproximación al marco fiscal, hemos tenido en cuenta este límite del 30% en los ejemplos realizados en el trabajo. Teniendo en cuenta estas cuestiones fiscales de carácter general, pasamos a describir la incidencia que tiene el método de amortización en el modelo.
3.1. AMORTIZACIÓN CONSTANTE
En este caso dividimos el importe de la inversión entre el número de años de vida útil del equipo productivo. Teniendo en cuenta las magnitudes presentadas en la tabla 2 y desarrollando el concepto de recurso generado podemos escribir:
La expresión general del VAN viene dada por:
Siendo, k = r si la financiación es propia y k = r(1-t) si la financiación es ajena. Sustituyendo [1] en [2] y simplificando, queda la siguiente expresión de VAN:
Anulando [3] y despejando Q obtenemos la cantidad de producto anual:
Por ejemplo, para I = 20000, n = 5, p = 10, Cvme = 2, CF = 2000, t = 0,2 y r = k = 0,05 (caso de financiación propia), obtenemos Q = 846,8 unidades de producto. Si la financiación fuese ajena, entonces k = 0,05(1 - 0,2) = 0,04 y Q = 826,9 unidades de producto. Al bajar el coste de la financiación es necesaria una menor cantidad anual de producto para anular el VAN.
3.2. AMORTIZACIÓN SEGÚN DÍGITOS CRECIENTES
El método de dígitos crecientes consiste en asignar un número dígito a cada uno de los años de vida útil del equipo productivo. Se suman los números dígitos y la amortización del primer año es el resultado de multiplicar el importe de la inversión I por 1/∑dígitos. La del segundo año, el resultado de multiplicar el importe de la inversión I por 2/∑dígitos y así sucesivamente. Es decir, la amortización para cada año viene dada por A1 = I/∑dígitos, A2 = 2I/∑dígitos,…, An = nI/∑dígitos. Como que la amortización es distinta para cada año, el recurso generado también lo es. Teniendo en cuenta [1] y que la suma de dígitos es ((n+1)/2)n, el recurso generado anual viene dado por:
Sustituyendo en [2] y simplificando queda:
Teniendo en cuenta el valor de la suma de los términos entre paréntesis, simplificamos la expresión anterior[7]:
Anulando [6] y despejando Q obtenemos la cantidad de producto anual:
[7]
Ahora, para anular el VAN de la inversión, son necesarias 850,8 unidades anuales de producto en el caso de financiación propia y 830,2 unidades en el caso de financiación ajena.
3.3. AMORTIZACIÓN SEGÚN DÍGITOS DECRECIENTES
Los números dígitos son n, n-1,…, 1, y la amortización para cada año viene dada por A1= nI/∑dígitos, A2 = (n-1)I/∑dígitos,…, An = I/∑dígitos. Reformulando [5] obtenemos:
Teniendo en cuenta el valor de la suma de los últimos términos entre paréntesis (ahora la diferencia entre numeradores es –tI), simplificamos la expresión anterior:
Igualando a cero la expresión [9] y despejando Q, obtenemos nuevamente la cantidad que anula el VAN de la inversión:
Como cabía esperar, la cantidad es menor que en los dos casos anteriores, ahora con 842,7 unidades anuales de producto en financiación propia y 823,7 unidades anuales de producto en financiación ajena, anulamos el VAN.
Utilizando los datos del ejemplo propuesto, ha sido calculado el VAN de las expresiones [3], [6] y [9] para valores seleccionados de Q, según que la financiación sea propia o ajena. Los resultados obtenidos son presentados en las tablas 3 y 4.
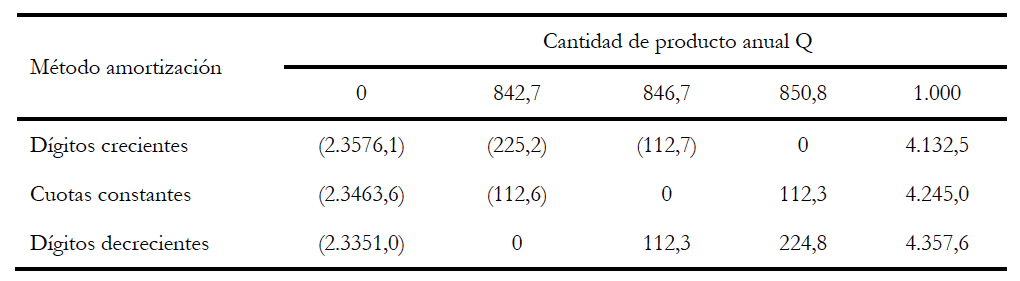
Tabla 3. VAN para valores de Q según amortización (financiación propia)
Fuente: Elaboración propia.
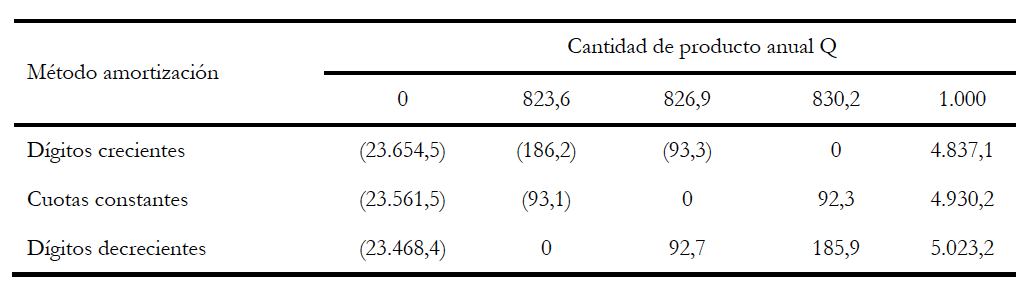
Tabla 4. VAN para valores de Q según amortización (financiación ajena)
Fuente: Elaboración propia.
En estas tablas se observa que el VAN crece con la cantidad de producto anual. También, que la amortización por dígitos decrecientes es la más favorable, ya que en ambos tipos de financiación recuperamos la inversión con una menor cantidad de producto. O lo que es lo mismo, para una misma cantidad de producto anual, el VAN es mayor. El caso más desfavorable es que corresponde a la amortización por dígitos crecientes. El caso correspondiente a la amortización por cuotas constantes se sitúa entre los dos anteriores.
La relación lineal entre el VAN y la cantidad de producto anual queda patente en los tres métodos de amortización y para ambos tipos de financiación. En la figura 1 observamos dicha relación en el caso de financiación propia, según los tres métodos de amortización.
Figura 1. VAN y cantidad de producto según amortización (financiación propia)
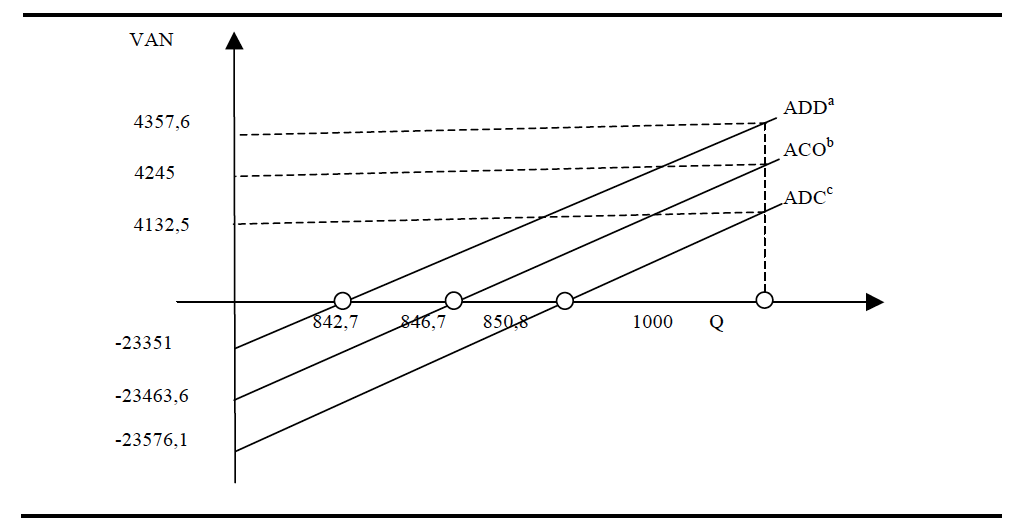
Nota: a amortización dígitos decrecientes. b amortización cuotas constantes. c amortización dígitos crecientes.
Como podemos comprobar el VAN aumenta en una cuantía fija cuando pasamos del método de dígitos crecientes al constante y de éste al método de dígitos decrecientes. Y un comportamiento análogo al que aparece en la figura anterior se observaría en caso de financiación ajena.
Por otra parte, si analizamos la relación entre VAN y Q en las expresiones [3], [6] y [9], constatamos una relación lineal cuya pendiente es (p - Cvme)(1 - t)аn,k; observándose que es mayor en el caso de financiación ajena,(k=0,04) que en el caso de financiación propia (k=0,05). Así, cuando para un mismo método de amortización analizamos la relación entre VAN y Q según tipo de financiación, comprobamos que las rectas, partiendo de distintas ordenadas en el origen, se cortan posteriormente, para a continuación mantener ventaja siempre la financiación ajena. Esto puede observarse en la figura 2.
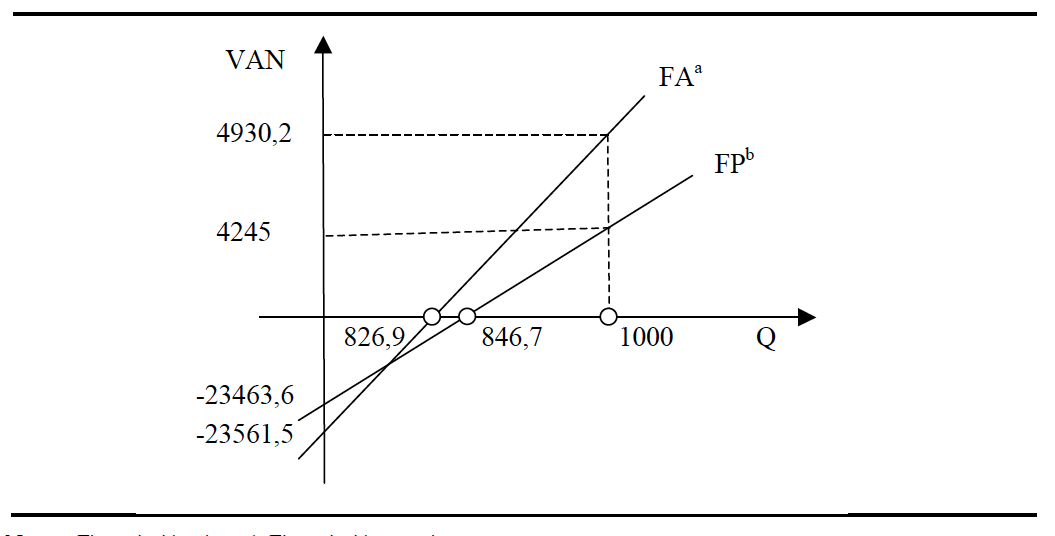
Figura 2. VAN y cantidad de producto según financiación (amortización constante)
Nota: a Financiación ajena. b Financiación propia
Y un comportamiento análogo al observado en la figura 2 se daría con los otros dos métodos de amortización.
3.4. RELACIÓN ENTRE LOS MODELOS ANTERIORES Y EL PUNTO DE EQUILIBRIO CONTABLE
Como es sabido el punto de equilibrio contable se define como aquella cantidad de producto o nivel de ingresos que anulan el beneficio. Tanto en el caso del punto de equilibrio en cantidad como en ingresos, se parte de una clasificación de los costes, en fijos y variables. Los primeros son independientes de la producción, los segundos no. El punto de equilibrio en ingresos viene dada por IN-CV-CF = 0; pero como buscamos la cantidad de equilibrio, escribimos pQ-CvmeQ-CF = 0, con lo que Q = CF/(p-Cvme)[8]. En realidad, el punto de equilibrio contable es un caso particular del modelo desarrollado anteriormente, cuando k = 0; es decir, cuando no tenemos en cuenta el valor del dinero en el tiempo. Efectivamente, observemos que las expresiones [3] y [4] contienen el factor de actualización аn,k que sólo está definido para k ≠ 0. Cuando k = 0, la expresión general del VAN se reduce a:
Con lo que teniendo en cuenta [1] y [3], podemos escribir:
Anulando la expresión anterior y despejando Q, queda:
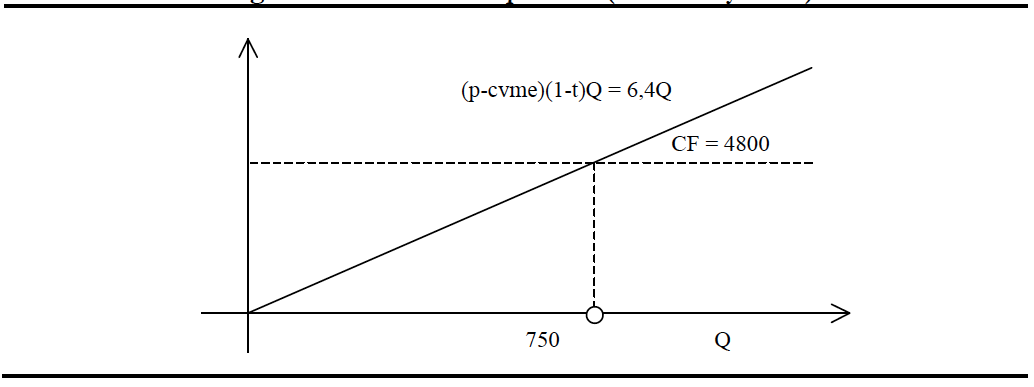
Cuya expresión se corresponde con la del punto de equilibrio contable tradicional corregido por el efecto de los impuestos. Substituyendo en nuestro ejemplo, obtenemos 750. Es decir, son necesarias 750 unidades anuales de producto para que el beneficio y el VAN sean nulos. Y como vemos, la cantidad es sensiblemente inferior a las cantidades obtenidas anteriormente, en que k > 0.
Y de la misma forma que hemos operado en el caso de las cuotas de amortización constantes, lo hacemos en el de amortización por dígitos crecientes. Tomando la expresión [5], sustituyendo k = 0 y simplificando obtenemos:
Igualando la expresión anterior a cero y despejando Q queda:
Sustituyendo con los valores de nuestro ejemplo, resulta Q = 750 unidades anuales de producto. E igualmente procederíamos con la amortización por dígitos decrecientes a partir de la expresión [8], obteniéndose la misma expresión de cálculo y la misma cantidad de producto.
En la figura siguiente representamos la cantidad anual de equilibrio correspondiente al ejemplo propuesto:
Figura 3. Cantidad de equilibrio (VAN = 0 y k = 0)
4. AMORTIZACIÓN SEGÚN PRODUCCIÓN
Cuantificar la depreciación de un equipo productivo es tarea compleja, pues aparte de que la depreciación es en realidad una variable continua en el tiempo, sus componentes son diversos, incluyendo no sólo el uso o servicio sino también todo tipo de obsolescencia tanto técnica como económica, lo que requiere a veces de técnicas complejas, incluidos los modelos econométricos. Un buen ejemplo es el que realizan Guadalajara y Fenollosa (2010), estimando la depreciación de la maquinaria agrícola en países del sur de Europa utilizando técnicas multivariantes y análisis de conglomerados. Desde esta perspectiva, en numerosas ocasiones, se ha querido profundizar en la naturaleza de la depreciación, intentando cuantificar que parte de la depreciación se debe al uso o servicio del propio equipo productivo y que parte se debe a la obsolescencia técnica y económica. En algunos equipos, la depreciación debida al uso o servicio debe ser importante. Entendemos que este criterio de amortización es recogido explícitamente en BOE (2014) cuando se refiere a otros criterios de amortización en los que el contribuyente se ajuste a un plan específico que sea aceptado por la Administración, o cuando el contribuyente justifique su importe. Más concretamente este criterio es recogido en una resolución del Instituto de Contabilidad y Auditoría de Cuentas, (BOE, 2013).
Efectivamente, en referencia a los diferentes métodos de amortización dicha disposición expone: “…y el método de unidades de producción que supondrá un gasto por amortización basado en la utilización o producción esperada” (BOE, 2013: 18448). Y a continuación añade: “algunos bienes del inmovilizado material son objeto de agotamiento, tales como las minas. Estos bienes se amortizarán aplicando el método que mejor refleje el patrón con arreglo al cual se estima que vayan a ser consumidos. En particular las minas se amortizarán en función del tonelaje extraído o utilizando otros criterios racionales que se apoyen en bases firmes de gestión” (BOE, 2013: 18448).
En nuestra opinión, el método de amortización en función de las horas de servicio, los kilómetros recorridos o la producción puede ser adecuado en equipos industriales sujetos a una baja obsolescencia técnica o económica, como los equipos productivos de sectores agrícolas primarios[9], y no sería adecuado en los equipos informáticos y en general en los equipos relacionados con las nuevas tecnologías en los que la depreciación por obsolescencia puede ser prácticamente total[10].
En esta segunda parte del trabajo, introducimos una amortización en función de la cantidad de producto anual. Supondremos que dicha cantidad será primero constante y después variable, siguiendo en este segundo caso una ley geométrica creciente o decreciente. La amortización sobre producción anual constante equivale a la amortización constante, ya desarrollada anteriormente, con lo que recurso generado anual sería igual al obtenido en [1]. La amortización anual viene dada por:
Que tal como observamos equivale al método de cuotas de amortización constantes expuesto anteriormente, pudiéndose aplicar directamente la expresión [4]. Por ejemplo, para I = 1000, CF = 10, p = 30, Cvme = 5, n = 4, r = 0,1 y t = 0,4; obtenemos Q = 14,7 unidades anuales de producto con financiación propia y 12,9 unidades con financiación ajena[11]. Si la cantidad de producto varía cada año sin ningún tipo de regularidad, no podremos resolver el problema al existir infinitas soluciones.
4.1. AMORTIZACIÓN EN FUNCIÓN DE PRODUCCIÓN CRECIENTE SEGÚN LEY GEOMÉTRICA
La producción anual aumenta o disminuye según una determinada ley. Este sería el caso en el que determinados equipos productivos deben ajustar su capacidad de producción a unas especificaciones técnicas determinadas o también al caso de una demanda creciente, lo que podría suponer ir aumentando la producción anual en una determinada proporción. Si suponemos que dicha producción aumenta a la tasa acumulativa anual g, la cantidad Qi al final de cada año vendrá dada según Q1(1+g)i-1 (i =1, 2, …, n), y la suma de dichas cantidades anuales por:
Teniendo en cuenta lo anterior, el recurso generado en el año i viene dado por la siguiente expresión:
Eliminando Q1 en la segunda parte de la expresión y sustituyendo cada término en la expresión general del VAN [2], queda:
Igualando el VAN a cero y despejando Q1 queda finalmente:
[11]
Para el ejemplo anterior, con g = 0,08 y en el caso de financiación propia, obtenemos Q1 = 13,2 y teniendo en cuenta Q1(1+g)i-1, las cantidades de producto para cada uno de los años siguientes Q2 = 14,3; Q3 = 15,4 y Q4 = 16,7.
4.2. AMORTIZACIÓN EN FUNCIÓN DE PRODUCCIÓN DECRECIENTE SEGÚN LEY GEOMÉTRICA
En ocasiones, las condiciones tecnológicas del proceso productivo o las condiciones de la demanda nos conducen a una cantidad de producto que decrece anualmente. Si la producción anual disminuye a la tasa acumulativa anual –g, la cantidad de producto Qi obtenida al final de cada año viene dada por Q1(1-g)i-1 (para i =1, 2, …, n), y la suma de las cantidades anuales según:
Nuevamente, siguiendo el proceso desarrollado anteriormente, llegamos a la siguiente expresión de cálculo:
Anulando el VAN y despejando Q1, obtenemos:
[12]
Ahora, con g = -0,08 obtenemos Q1 = 16,4 y teniendo en cuenta la expresión general Q1(1-g)i-1, las cantidades para los años siguientes son Q2 = 15,1; Q3 = 13,8 y Q4 = 12,7.
Como hemos señalado, el coste de la financiación ajena es del 6% anual, con lo que la cantidad de producto anual que anule el VAN debe ser menor que en los casos anteriores. Con producción creciente dichas cantidades son Q1 = 11,6; Q2 = 12,5; Q3 = 13,5 y Q4 = 14,6; y con producción decreciente, Q1 = 14,5; Q2 = 13,3; Q3 = 12,2 y Q4 = 11,3.
5. RECURSOS GENERADOS CONTINUOS
En los apartados anteriores hemos supuesto que la producción y los recursos generados anuales correspondientes eran discretos en el tiempo; se obtenían en un momento determinado, concretamente al final de cada año. Por lo tanto, cada recurso generado era actualizado multiplicando su importe por el factor anual de interés compuesto (1+k)-i (i = 1, 2, …, n). Ahora bien, esto no es más que un convenio que puede reflejar un hecho concreto, pero que no siempre se cumple.
Un bono puede pagar interés al final de cada año y su titular podrá utilizar el factor de descuento mencionado para conocer el valor actual de los intereses cobrados. Pero generalmente una empresa no vende toda su producción al final de cada año, así como tampoco paga todos sus gastos. La producción y por lo tanto los ingresos correspondientes se irán generando de forma más o menos continua a lo largo del año. Ciertos gastos como los salarios suelen ser pagados al final de cada mes; otros gastos, cada día; por lo que en numerosas ocasiones una corriente monetaria continua a lo largo del año puede reflejar más fielmente una situación concreta[12]. Si además sustituimos el factor de descuento compuesto por el factor de descuento continuo o instantáneo, e-kn (lo que parece lógico, si tenemos en cuenta ahora que la corriente de dinero se genera de forma continua a lo largo del año), entonces estamos introduciendo el concepto de recurso generado continuo, capitalizado (actualizado) continuamente. Este es el supuesto que introducimos a continuación.
Ahora debemos adaptar las expresiones [4], [11] y [12] al caso en el que la producción anual y el recurso generado correspondiente son continuos. Primero lo haremos en el caso de producción anual constante y después en los casos de producción creciente y decreciente según ley geométrica.
En el caso [4] será necesario sustituir el factor аn,k por el factor correspondiente al valor actual de una unidad anual continua obtenida durante n años, actualizada a la tasa anual continua k. Dicho factor al que denominamos аcn,k, viene dado por[13]:
Este factor de actualización puede obtenerse también a partir del valor actual de una unidad anual obtenida durante n años dividida en m intervalos al año y actualizada a la tasa k/m, cuando el intervalo es suficientemente pequeño[if !supportFootnotes][14][endif]. Adaptando lo anterior a la expresión [4], queda:
[13]
Con financiación propia, para anular el VAN, son necesarias 13,9 unidades anuales cuando en el caso discreto eran necesarias 14,7 unidades. Con financiación ajena, son 12,4 y 12,9 unidades, respectivamente. Estos resultados son lógicos teniendo en cuenta que ahora la producción se obtiene a lo largo de cada año y antes se obtenía a final de cada año.
Para encontrar la cantidad de producto del primer año en el caso de producción creciente, hemos de readaptar la expresión [11] al caso continuo. En este caso modificamos las expresiones φn,g y аn,k,g por sus correspondientes en tiempo continuo φcn,g y аcn,k,g[15].
Nuevamente señalamos que φcn,g es el factor correspondiente al valor final de una unidad anual continua que crece a la tasa anual continua g durante n años. Mientras que аcn,k,g es el factor correspondiente al valor actual de una unidad anual continua que crece a la tasa anual continua g y es actualizada a la tasa anual continua k, durante n años. De igual modo, los dos factores anteriores pueden deducirse de la siguiente forma: a) en el primer caso, a partir de una unidad anual que es dividida en m intervalos cada año y capitalizada a la tasa continua g/m durante n años, cuando el intervalo es suficientemente pequeño (González, 2010), b) en el segundo caso, a partir de una unidad anual que es dividida en m intervalos al año creciendo a la tasa continua g/m y actualizada a la tasa continua k/m durante n años, cuando el intervalo es suficientemente pequeño (ver Anexo I).
Aplicando [14] obtenemos que para anular el VAN son necesarias el primer año 12 unidades de producto con financiación propia y 10,7 con financiación ajena, cuando en el caso discreto eran necesarias 13,3 unidades y 11, 6 unidades respectivamente.
Finalmente, para encontrar la cantidad de producto del primer año en el caso de producción decreciente, readaptamos la expresión [12] al caso continuo. Ahora modificaremos las expresiones φn,-g y аn,k,-g por las correspondientes en tiempo continuo φcn,-g y аcn,k,-g[16]. Dicha expresión final viene dada por:
De igual modo, las expresiones φcn,-g y аcn,k,-g pueden ser deducidas a partir de las correspondientes expresiones discretas. En el primer caso, a partir de una unidad anual durante n años, dividida en m intervalos al año y capitalizada a la tasa continua –g/m, cuando el intervalo es suficientemente pequeño (ver Anexo II). En el segundo caso, a partir del valor de una unidad anual durante n años, dividida en m intervalos al año, decreciendo a la tasa continua –g/m y actualizada a la tasa continua k/m, cuando el intervalo es suficientemente pequeño (ver Anexo III).
En nuestro ejemplo propuesto y aplicando [15], obtenemos que mientras que para el primer año en el caso discreto eran necesarias 16,4 unidades de producto con financiación propia y 14,5 unidades con financiación ajena, en el caso continuo son necesarias 16 unidades y 14,4 unidades respectivamente.
Como resumen de lo anterior podemos concluir que para anular el VAN de la inversión siempre es necesario obtener menor cantidad de producto anual en el caso continuo que en el caso discreto, y esto se cumple tanto para los distintos métodos de amortización como para los distintos tipos de financiación.
6. CONCLUSIONES FINALES
Después de resaltar la importancia del análisis de sensibilidad como instrumento para introducir el riesgo en una inversión, hemos desarrollado un modelo en el que sometemos a variabilidad la cantidad de producto anual con el fin de cuantificar su efecto en el VAN. En nuestro caso, este análisis de sensibilidad se concreta en determinar la cantidad de producto anual que anula el VAN de la inversión, introduciendo el concepto de recurso generado en función del criterio de amortización utilizado.
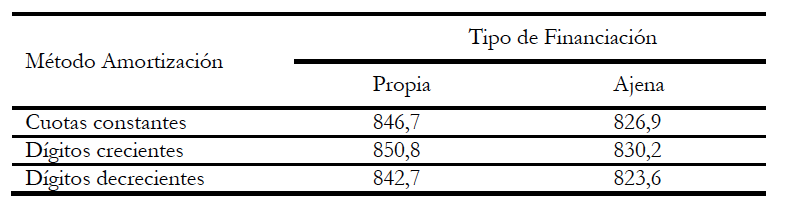
En el primer supuesto, en el que la amortización depende del importe de la inversión y de la vida útil del equipo productivo según tres métodos de amortización (cuotas de amortización constantes, dígitos crecientes y dígitos decrecientes), obtenemos que la cantidad anual de producto necesaria para anular el VAN es menor cuando amortizamos por dígitos decrecientes que cuando lo hacemos por dígitos crecientes, situándose la cantidad obtenida por cuotas de amortización constantes en una posición intermedia. Como era de esperar, las cantidades que anulan el VAN son menores con financiación ajena que con financiación propia (para una misma tasa nominal de dividendos/interés, y siempre que la tasa impositiva sobre beneficios sea positiva). Un resumen sintético de lo afirmado en estas líneas, puede observarse en la tabla 5.
Tabla 5. Cantidad de producto que anula el VAN
Fuente: Elaboración propia.
Esta ventaja del VAN en el caso de financiación ajena es independiente del método de amortización utilizado, ya que la pendiente de la función de VAN en relación a la cantidad de producto anual es mayor con financiación ajena. Dicha ventaja va acusándose cada vez más a medida que aumentamos la cantidad de producto. En otras palabras, siempre es necesaria una menor cantidad anual de producto para anular el VAN en el caso de financiación ajena.
Finalizamos esta primera parte relacionando los modelos anteriores con el punto de equilibrio contable. Efectivamente, cuando en los modelos anteriores incluimos el supuesto de que k = 0, obtenemos un único modelo que coincide con el tradicional punto de equilibrio contable. En este caso, al tratarse de un modelo estático, en el que no se tiene en cuenta el valor del dinero en el tiempo, la cantidad anual de producto necesaria para anular el VAN es siempre menor.
En el segundo supuesto, en el que la amortización depende de la producción anual, (tanto creciente como decreciente, según ley geométrica), siempre es necesaria una menor cantidad anual de producto para anular el VAN en el caso de financiación ajena. Cuando suponemos que la producción anual es constante, obtenemos el modelo ya desarrollado anteriormente de amortización constante, cuya cantidad anual de producto necesaria para anular el VAN se sitúa entre las dos anteriores. También en este caso, para anular el VAN de la inversión, se necesita una menor cantidad de producto con financiación ajena.
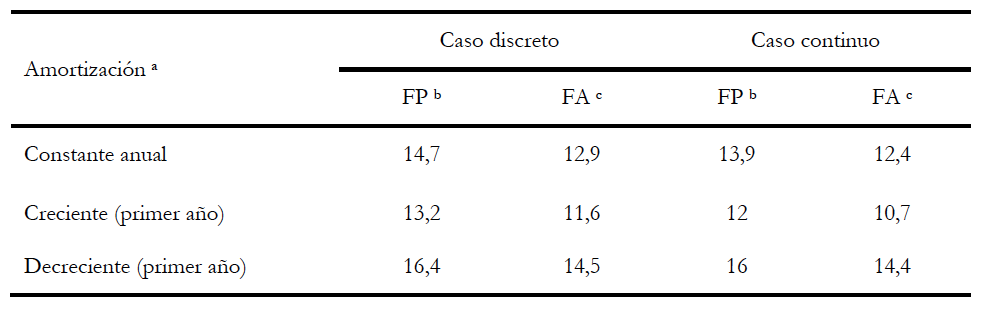
Cuando introducimos el supuesto de que la producción es continua en el tiempo, la cantidad anual necesaria para anular el VAN es siempre menor que en el caso discreto. Esto se cumple cuando la cantidad de producto es constante cada año y también para el primer año cuando la producción es creciente o decreciente según determinada ley geométrica. Este hecho se cumple tanto con financiación propia como con financiación ajena. En la tabla 6 se presenta un resumen sintético de lo comentado en estos dos últimos párrafos.
Tabla 6. Cantidad de producto que anula el VAN
Fuente: Elaboración propia.
Nota: a Amortización según cantidad de producto. b Financiación propia. c Financiación ajena.
Los resultados obtenidos en este trabajo son coincidentes con los obtenidos en otros trabajos análogos. En concreto el realizado por Ferruz y Alda (2010) en el que utilizando distintos métodos de amortización, se concluye que los métodos de amortización acelerados aportan un VAN mayor como consecuencia de los ahorros fiscales actualizados. Además, cuando introducimos en el modelo el supuesto de que la tasa de descuento es nula, los resultados obtenidos coinciden con los que obtiene Tarsia (2007); el cual, al analizar la sensibilidad de la cantidad de producto anual en relación a la tasa de descuento, llega a la conclusión de que dicha cantidad tiende a ser la misma que la cantidad de equilibrio (punto de equilibrio contable), cuando la tasa de descuento se aproxima a cero. Por otra parte, y aunque no hemos encontrado referencias bibliográficas concretas, los resultados son consecuentes con el efecto que sobre el VAN y la cantidad de producto anual cabría esperar de una financiación con un menor coste de capital y de una producción continua en el tiempo.
ANEXO
En los apartados siguientes, una vez que ha sido obtenida la expresión general correspondiente, aplicamos la Regla de L’Hôpital y posteriormente hacemos m=∞
ANEXO I
ANEXO II
ANEXO III
Notas
REFERENCIAS
Alegre, L., Berné, C., y Galve, C. (2000). Fundamentos de economía de la empresa: perspectiva funcional. Ariel Economía, Barcelona.
BOE, (2013). Resolución de 1 de marzo de 2013, del Instituto de Contabilidad y Auditoría de Cuentas, por la que se dictan normas de registro y valoración del inmovilizado material y de las inversiones inmobiliarias, 58, Madrid.
BOE (2014). Ley 27/2014, de 27 de Noviembre, 88, Madrid.
Brealey, R., Myers, S., and Allen, F. (2014). Principles Of Corporate Finance. Mc Graw Hill Education, New York.
Calleja, J.L. (2008). Concepto de amortización elementos del inmovilizado. IE Business School, Madrid.
Cañibano, L. (1996). Contabilidad. Análisis contable de la realidad económica. Pirámide, Madrid.
Ferruz, L., y Alda, M. (2010). Valoración de las amortizaciones fiscalmente deducibles. Análisis Financiero, 113: 60-70.
Gil, E. (2001). Elección correcta de la maquinaria agrícola. Agrotécnica, 4, 167-175.
González, J.L. (2010). Empresa: marco conceptual y técnicas de gestión por áreas funcionales. Materials, 218, UAB, Bellaterra.
Guadalajara, M.N., y Fenollosa, M.L. (2010). Modelos de valoración de maquinaria agrícola en el sur de Europa. Un análisis de la depreciación real. Agrociencia, 44, (3): 381-391.
Menéndez, C., y Montllor, J. (1991). Planificación financiera y análisis de viabilidad de inversiones por medio de proyectos agregados: el valor final neto. Técnica Contable, 43, (514): 563-582.
Montllor, J. (1986). La sensibilidad de las decisiones de inversión ante variaciones sistemáticas de los flujos de caja. Investigaciones Económicas, X, (1), 141-162.
Pascual, J. (2007). Los criterios Valor Actual Neto y Tasa Interna de Rendimiento. E-pública, 2: 1-11.
Sánchez, J.L. (2008). Teoría y práctica de la contabilidad. Pirámide, Madrid.
Sapag, N. (2004). Evaluación de proyectos de inversión en la empresa. Pearson Education-Prentice Hall, Buenos Aires.
Suárez, A.S. (2005). Decisiones óptimas de inversión y financiación en la empresa. Pirámide, Madrid.
Tarzia, D.A. (2007). El punto muerto financiero de un proyecto de inversión simple en función de la tasa de descuento. Mecánica computacional, XXVI, octubre: 614-632.
Vergés, J. (1994). La planificació econòmica i financera a l’empresa. Elaboració i utilització de previsions com a base de la gestió. Manuals de la Universitat Autònoma de Barcelona, 17, Bellaterra.
Villazón, C., y Sanou, L. (1993). Matemática financiera. Ediciones Foro Científico, Barcelona.