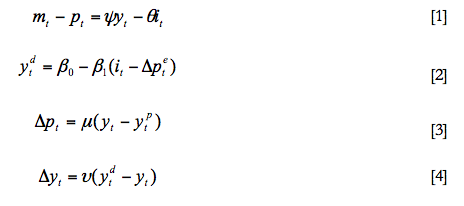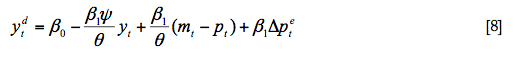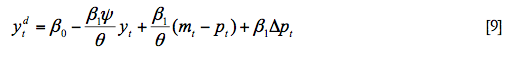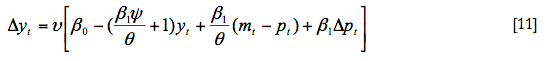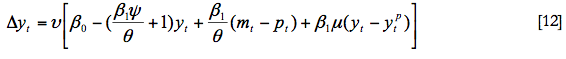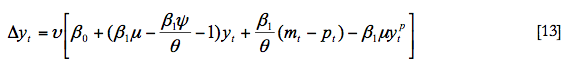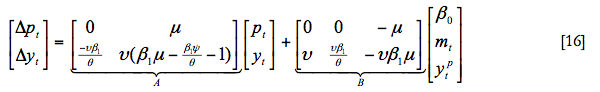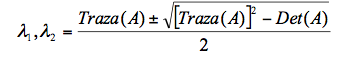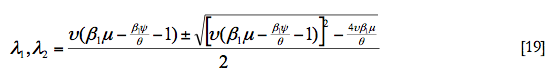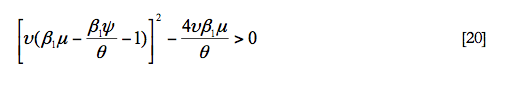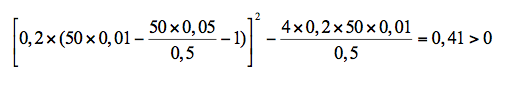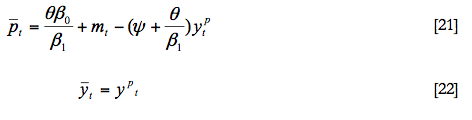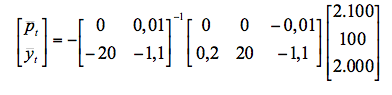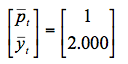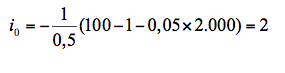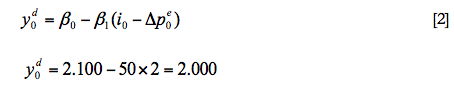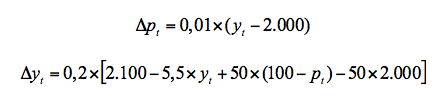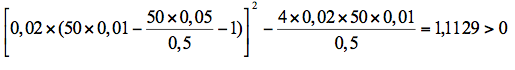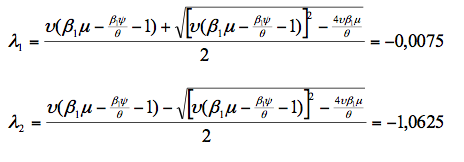1.INTRODUCCIÓN
La macroeconomía actual tiene como uno de sus elementos fundamentales de análisis la resolución y simulación de modelos de equilibrio general dinámicos estocásticos. Este tipo de modelos, que están basados en la micro-fundamentación de las decisiones que toman los distintos agentes económicos, se han convertido en el eje principal del análisis macroeconómico actual, teniendo dos características fundamentales: se trata de modelos dinámicos y la modelización se realiza en un entorno de equilibrio general. Sin embargo, al margen de la mayor o menor complejidad teórica que presentan este tipo de modelos, el principal problema que presentan para su enseñanza a los alumnos de Grado en Economía es que no tienen una solución explícita, por lo que únicamente pueden ser resueltos de forma numérica, lo que supone una importante barrera para su incorporación a las asignaturas de macroeconomía avanzada en los Grados de Economía. Incluso la enseñanza de modelos macroeconómicos dinámicos simples requiere el uso de instrumentos de análisis relativamente complejos, tal y como trabajar con sistemas de ecuaciones en diferencias o ecuaciones diferenciales. En todos esos casos, la estrategia consiste en aplicar el análisis gráfico, a través de la construcción del diagrama de fases, como instrumento básico para la realización de análisis macroeconómico. No obstante, incluso la utilización del diagrama de fases supone un cierto nivel de dificultad, al tiempo que presenta ciertas limitaciones. Sin embargo, una hoja de cálculo contiene herramientas que pueden ser usadas de forma sencilla en la resolución numérica de modelos macroeconómicos relativamente simples.
El presente documento forma parte de un manual, titulado Macroeconomía Computacional (en prensa), elaborado por los autores y cuyo objetivo primordial es realizar una introducción, al nivel más básico posible, a la Macroeconomía Computacional. Este manual comprende una serie de ejercicios de computación, usando diferentes desarrollos teóricos y que se dividen en tres partes: Modelos Dinámicos Básicos, Equilibrio General Dinámico y Crecimiento Económico. El objetivo es resolver diferentes modelos teóricos muy sencillos pero utilizando técnicas de resolución numéricas y de computación en una hoja de cálculo como Excel. A partir de la elaboración de unas sencillas hojas de cálculo es posible obtener una resolución numérica de diferentes modelos, obteniéndose las funciones impulso-respuesta ante distintas perturbaciones. En este documento presentamos uno de los ejercicios realizados, consistentes en la simulación numérica de una versión dinámica del modelo IS-LM.
El programa informático que hemos utilizado para la resolución de ejercicios en este manual ha sido Excel. Excel es una hoja de cálculo, similar a otras como puede ser la hoja de cálculo Calc de Open Office. Las ventajas de una hoja de cálculo es que son fáciles de manejar, ampliamente utilizadas, al tiempo que tienen una capacidad muy elevada para realizar una gran variedad de operaciones de cálculo. Barreto (2015) presenta una serie de argumentos de porqué Excel es una herramienta adecuada para la enseñanza de la macroeconomía. De hecho las hojas de cálculo son un recurso que está siendo cada vez más utilizado en la enseñanza de la economía, siendo ejemplos Strulik (2004), Gilbert y Oladi (2011) y Del Rey y Silva (2012). Más recientemente Barreto (2016) propone un conjunto de hojas de cálculo para la enseñanza de la macroeconomía a niveles introductorios e intermedios. Tal y como indica Barreto (2016), las hojas de cálculo presentan importantes ventajas a la hora de comunicar ideas y de presentar datos estadísticos a los estudiantes. Otro manual de macroeconomía que ofrece la simulación en Excel de los modelos estudiados es el de Carlin y Soskice (2015). Finalmente, un manual donde también se utilizan otros programas informáticos, al margen de hojas de cálculo, es Kendrick, Mercado y Amman (2006).
La necesidad de utilizar este nuevo enfoque proviene del hecho de que la interrelación entre la macroeconomía actual y las herramientas de computación es muy estrecha. El modelo teórico de referencia que se emplea en el análisis macroeconómico moderno es el denominado modelo de Equilibrio General Dinámico Estocástico o modelo de crecimiento óptimo de Ramsey, el cual no tiene una solución cerrada y por tanto solo puede resolverse utilizando métodos numéricos. Esto hace que la Macroeconomía Computacional sea una pieza clave en el análisis económico actual y resulte necesario un cambio de enfoque en la forma en la que se introduce a los alumnos en el análisis macroeconómico a un nivel avanzado.
Los modelos macroeconómicos dinámicos pueden escribirse en términos generales como un sistema de ecuaciones diferenciales o en diferencias, dependiendo si definimos dicho modelo bajo un contexto de tiempo continuo (si el objetivo es utilizar un diagrama de fases) o tiempo discreto (si el objetivo es su resolución numérica). A nivel teórico, los modelos macroeconómicos dinámicos se han resuelto tradicionalmente considerando un contexto de tiempo continuo, lo que supone trabajar con ecuaciones diferenciales. Esto es así porque el principal instrumento para el análisis macroeconómico que se utiliza en este marco teórico es el diagrama de fases. Sin embargo, la resolución en términos numéricos requiere pasar del tiempo continuo al tiempo discreto. Por tanto, en lugar de trabajar con ecuaciones diferenciales trabajaríamos con ecuaciones en diferencias, siendo ambos enfoques equivalentes respecto a los resultados obtenidos.
Resolver numéricamente este tipo de sistemas tiene importantes ventajas. En primer lugar, permite la obtención de las sendas temporales de las variables, que no se pueden apreciar de forma directa en los diagramas de fases. Así, basta con realizar un gráfico del valor de cada variable en función del tiempo para apreciar su comportamiento a lo largo del mismo. De este modo es posible derivar las denominadas funciones impulso-respuesta de las diferentes variables macroeconómicas ante una determinada perturbación. En segundo lugar, permite realizar ejercicios de sensibilidad, estudiando el comportamiento del sistema en función, tanto del valor de las variables exógenas como del valor de los distintos parámetros. Así, una vez resuelto el modelo y computado numéricamente, basta, por ejemplo, con cambiar el valor de un determinado parámetro para ver cómo la economía se ve alterada, tanto en términos de su equilibrio como de su dinámica. Esto significa que podemos simular las distintas trayectorias de las variables endógenas, dados unos parámetros y una determinada perturbación en las variables exógenas. Estos elementos no son posibles de apreciar resolviendo el sistema de forma teórica y representándolo a través del correspondiente diagrama de fases.
La estructura que vamos a seguir en el presente documento es la siguiente. En el segundo apartado presentamos una breve descripción de las ecuaciones que componen el modelo a resolver numéricamente. La sección tercera muestra la resolución numérica de dicho sistema dinámico realizada en una hoja de Excel, describiéndose todos los elementos que deben introducirse en la hoja de cálculo para obtener la solución numérica del mismo. La sección cuarta utiliza la hoja de cálculo construida anteriormente para analizar los efectos de una determinada perturbación, es decir, un cambio en las variables exógenas, a partir del cual obtenemos las funciones impulso-respuesta para las variables endógenas. La sección quinta realiza un análisis similar pero en términos de un cambio en el valor de los parámetros. A esto es a lo que se denomina análisis de sensibilidad. Finalizaremos con algunas conclusiones.
2.UN MODELO IS-LM DINÁMICO
A continuación vamos a usar una versión dinámica del modelo IS-LM, dado que se trata del modelo que continúa constituyendo el núcleo central de la enseñanza de la macroeconomía a nivel introductorio/intermedio. Aunque sería más apropiado el uso de un modelo tipo IS-RM, con una regla de política monetaria, que se adapta mejor a la modelización del funcionamiento del mercado de dinero, esta especificación aún es poco utilizada en la práctica de la enseñanza de la macroeconomía, por lo que hemos optado por presentar la versión tradicional ampliamente conocida. Incluso, los manuales de macroeconomía más actuales siguen centrándose en el modelo tradicional basado en la curva LM (una excepción es el manual de Bajo y Díaz, 2011, en el cual el modelo utilizando a lo largo del mismo se basa en el enfoque de la regla monetaria).
El modelo IS-LM presenta una gran cantidad de limitaciones, aunque también produce resultados de interés a nivel macroeconómico. De hecho, en el ejercicio que se muestra (si bien se trata de un modelo IS-LM dinámico, con propiedades muy distintas al tradicional IS-LM estático con precios fijos), se muestra la neutralidad monetaria en el largo plazo, si bien a corto y medio plazo una perturbación de carácter nominal tiene efectos reales sobre la economía. Pasar de una versión estática a una dinámica en términos de Oferta Agregada-Demanda Agregada resulta relativamente sencillo, para lo cual necesitamos especificar la dinámica que siguen tanto los precios como el nivel de producción. Para ello vamos a suponer que la estructura de nuestra economía viene dada por el siguiente sistema de ecuaciones:
donde m es el logaritmo de la cantidad de dinero, p el logaritmo del nivel de precios, yd el logaritmo del nivel de demanda, y el logaritmo del nivel de producción, yP el logaritmo del nivel de producción potencial, y finalmente i el tipo de interés nominal. El símbolo Δ define la variación de la variable correspondiente, siendo:
Nótese que al suponer que todas las variables vienen definidas en términos logarítmicos Δyt, es a lo que denominamos crecimiento del PIB y Δpt es a lo que denominamos inflación.
La ecuación [1] es la condición de equilibrio en el mercado de dinero donde los saldos reales, mt–pt (recordemos que las variables vienen definidas en términos logarítmicos), dependen positivamente del nivel de producción y negativamente del tipo de interés nominal. La ecuación [2] representa la demanda agregada de la economía, que depende positivamente del gasto público (o del componente autónomo de la misma) y negativamente del tipo de interés real. El tipo de interés real viene representado por la aproximación a la ecuación de Fisher y se obtiene como la diferencia entre el tipo de interés nominal y la tasa de inflación esperada.
Al margen de las dos ecuaciones de equilibrio para los dos mercados considerados, el modelo también está compuesto por otras dos ecuaciones dinámicas que nos indican el comportamiento de dos variables endógenas (nivel de precios y nivel de producción) ante situaciones de desequilibrio. Así la ecuación [3] nos indica cómo se mueven los precios en el tiempo en función de las diferencias entre el nivel de producción y el nivel de producción potencial. Si el nivel de producción es mayor al potencial, entonces dicha ecuación es positiva, por lo que los precios aumentan (inflación positiva). Por el contrario, si el nivel de producción es inferior al potencial, la ecuación tendría signo negativo, indicando que los precios disminuirían. Finalmente, la ecuación [4] es similar, mostrando la dinámica del nivel de producción. Así, esta expresión nos indica cómo se mueve el nivel de producción de la economía (la tasa de crecimiento de la economía) ante diferencias entre la oferta y la demanda agregada. Si el nivel de demanda agregada es superior al nivel de producción, la expresión tomaría un valor positivo, indicando que el nivel de producción aumenta. Por el contrario, si el nivel de producción es superior a la demanda, entonces la expresión tomaría un valor negativo, por lo que disminuiría el nivel de producción de la economía.
Todos los parámetros se definen en términos positivos. El parámetro ψ representa la elasticidad de la demanda de dinero respecto al nivel de producción, mientras que θ es la semi-elasticidad de la demanda de dinero respecto al tipo de interés nominal. Es una semi-elasticidad porque todas las variables del modelo vienen definidas en términos logarítmicos, excepto el tipo de interés, que al ser un porcentaje no le podemos aplicar logaritmos. El parámetro β1 representa la elasticidad del nivel de demanda agregada respecto al tipo de interés real, mientras que β0 es el componente autónomo de la demanda agregada, que vamos a suponer que refleja el gasto público. El parámetro μ nos indica la velocidad de ajuste de los precios ante diferencias entre el nivel de producción y el nivel de producción potencial. Por último, el parámetro υ nos indica la velocidad de ajuste del nivel de producción ante diferencias entre el nivel de demanda agregada y el nivel de producción de la economía.
En principio, y aunque se trata de una versión dinámica del modelo IS-LM, realmente estamos considerando el modelo de Oferta Agregada-Demanda Agregada, presentando algunas características importantes respecto al modelo estándar. Así, el modelo IS-LM es un modelo estático, donde los precios son constantes. Esto no es así en el modelo que estamos presentando, donde la dinámica de los precios, es decir, su variabilidad a lo largo del tiempo, juega un papel fundamental. Por otra parte, la demanda agregada es una función de las expectativas de inflación, que tampoco están presentes en el modelo IS-LM. Finalmente, los ajustes en las variables no son instantáneos, sino que tanto precios como nivel de producción se ajustan lentamente ante situaciones de desequilibrio. Estos elementos, junto con la consideración del tiempo, hacen que este modelo, a pesar de su simplicidad, sea muy ilustrativo a la hora de explicar el comportamiento de una economía.
Tal y como podemos comprobar el modelo está identificado, ya que contamos con cuatro variables endógenas (producción, nivel de precios, demanda agregada y tipo de interés nominal). Por otra parte, el modelo incluye un total de tres variables exógenas (componente autónomo de la demanda agregada que lo interpretamos como gasto público, cantidad de dinero y nivel de producción potencial). Para trabajar con este modelo vamos a proceder de forma similar a como lo haríamos en el caso de que nuestro objetivo fuese obtener el diagrama de fases, obteniendo un sistema de dos ecuaciones en diferencias, en términos del nivel de precios y del nivel de producción, que constituyen nuestras variables endógenas de referencia. Estas dos ecuaciones, cuya representación gráfica daría lugar al diagrama de fases, son las que van a determinar la evolución de la economía a lo largo del tiempo. Para obtener estas dos ecuaciones, en primer lugar tenemos que resolver para el resto de variables endógenas. Estas variables endógenas, para las cuales tenemos que resolver, son el tipo de interés nominal y el nivel de demanda agregada. Para ello utilizamos las expresiones [1] y [2]. Para obtener el tipo de interés nominal, despejamos en la ecuación [1]:
Ya tenemos el valor del tipo de interés nominal en función de las variables endógenas de referencia (precios y producción) y de las variables exógenas (cantidad de dinero). Por tanto, ya hemos resuelto para el tipo de interés nominal.
A continuación, vamos a resolver para el nivel de demanda agregada. Tal y como podemos comprobar en la ecuación (2), la demanda agregada depende del tipo de interés nominal. Como éste ya lo tenemos calculado, lo que hacemos es sustituir (7) en (2), de forma que obtenemos:
La expresión anterior no es una solución, dado que aún no podemos conocer el valor de la demanda agregada. En efecto, en la parte derecha de la ecuación aparece un término que, a priori, es desconocido. Se trata de las expectativas de inflación en el futuro. Este término aparece como consecuencia del cálculo del tipo de interés real. El tipo de interés real es una variable no conocida, dado que depende de la inflación que existirá al final del periodo de maduración al que esté referido el tipo de interés nominal correspondiente. Esto quiere decir que la demanda agregada tampoco es conocida excepto en términos esperados, ya que va a depender de las expectativas de inflación.
Por tanto, y como paso intermedio, hemos de proceder a resolver el término de expectativas, que en nuestro contexto va a ser muy sencillo. Para resolver las expectativas suponemos que estas son racionales. Es decir, la esperanza matemática de la inflación es igual a la inflación más un ruido blanco. Por otra parte, vamos a suponer que no existe incertidumbre, por lo que estaríamos en un contexto de previsión perfecta. Esto quiere decir que el ruido blanco, el término de error, de las expectativas racionales siempre es cero, por lo que el valor esperado de una variable en el futuro es el valor actual. En este caso la inflación esperada es simplemente la inflación actual (Δpt=Δpet). Por tanto, la ecuación que determina la demanda agregada de la economía sería:
Para obtener las dos ecuaciones dinámicas que van a determinar el comportamiento de nuestra economía, tenemos que sustituir en las ecuaciones de ajuste de las variables endógenas de referencia (nivel de precios y nivel de producción) el resto de variables endógenas, esto es el tipo de interés y el nivel de demanda agregada, que hemos obtenido anteriormente. En el caso de la ecuación dinámica para el nivel de precios, no aparecen dichas variables, por lo que esta primera ecuación es exactamente igual a la que proporciona el modelo:
A continuación, obtenemos la ecuación dinámica para el nivel de producción. Para ello sustituimos el valor obtenido para la demanda agregada en la ecuación dinámica del nivel de producción:
Como podemos observar, en la ecuación anterior aparece la inflación, es decir, la variación de los precios. El valor de la inflación viene dado por la ecuación de ajuste de los precios. Por tanto, tenemos que sustituir la ecuación (3) en la expresión anterior, obteniendo
Operando para agrupar términos y calcular el parámetro asociado a cada una de las variables endógenas de referencia y a las variables exógenas resulta:
Por tanto, el modelo queda reducido al siguiente sistema de dos ecuaciones:
En notación matricial tendríamos:
donde A es la matriz de coeficientes asociados a las variables endógenas y B la matriz de coeficientes asociados a las variables exógenas.
3. RESOLUCIÓN NUMÉRICA DEL MODELO
Una vez definidas las ecuaciones dinámicas que determinan la evolución a lo largo del tiempo de los precios y del nivel de producción, para poder trabajar numéricamente con este modelo necesitamos previamente dar valores a los parámetros. Estos valores se obtienen mediante de la realización de estimaciones econométricas o bien a través de la calibración de los mismos en función de los datos. Los valores de los parámetros pueden ser muy diferentes de una economía a otra, reflejando las características de las mismas en términos de la velocidad de ajuste de los parámetros. En nuestro caso, vamos a darle valores arbitrarios a dichos parámetros.
A la hora de fijar el valor de los parámetros tenemos que asegurarnos que cumplen determinadas condiciones. Una primera condición que les vamos a exigir es que las raíces de la matriz de coeficientes asociados a las variables endógenas sean números reales. En segundo lugar, tenemos que ver si el análisis de estabilidad impone alguna condición adicional sobre el valor de los mismos, con el objetivo de evitar disponer de un sistema en el cual todas las trayectorias sean explosivas. Para calcular los valores propios asociados a la matriz A, tenemos que resolver la siguiente ecuación:
donde I es la matriz identidad. Operando en la expresión anterior, obtendríamos la siguiente ecuación de segundo grado:
donde Traza(A) es la traza de la matriz A y Det(A) es su determinante. Resolviendo obtendríamos:
O bien
La primera condición que imponemos implica que tiene que cumplirse que:
En segundo lugar, el signo de los valores propios depende del signo de la traza de la matriz A. En este sentido, hemos de tener en cuenta que si el término β1μ-(β1ψ/θ)-1 es positivo, entonces las dos raíces son también positivas (λ1>0, λ2>0). En este caso todas las trayectorias serían explosivas por lo que el modelo no tendría sentido en términos económicos ya que ante una perturbación, la economía se alejaría permanentemente de su estado estacionario. Esto significa que esta combinación de parámetros no puede ser negativa. Si por el contrario β1μ-(β1ψ/θ)-1 es negativo entonces las dos raíces son negativas (λ1<0, λ2<0), siendo todas las trayectorias convergentes hacia el estado estacionario (estabilidad global) si las raíces toman valores mayores que -2. Así, podemos comprobar que para que las trayectorias sean convergentes al estado estacionario, no solo es necesario que ambas sean negativas, sino que tienen que ser mayores que -2.
Teniendo en cuenta las condiciones anteriores, los valores de los parámetros que vamos a utilizar en nuestro ejercicio aparecen en la Tabla 1.
Tabla 1. Valores de los parámetros
Símbolo |
Parámetros |
Valor |
| θ |
Semi-elasticidad de la demanda de dinero respecto al tipo de interés |
0,5 |
| ψ |
Elasticidad de la demanda de dinero respecto a la producción |
0,05 |
| β1 |
Elasticidad de la demanda agregada respecto al tipo de interés real |
50 |
| μ |
Velocidad de ajuste de los precios |
0,01 |
| υ |
Velocidad de ajuste del nivel de producción |
0,2 |
Sustituyendo los valores de la tabla 1 en la expresión [17] resulta que:
por lo que nos aseguramos que ambas raíces son reales. Por otro lado, también sabemos que el término β1μ-(β1ψ/θ)-1 tiene que ser negativo. Sustituyendo los valores dados en la tabla 1 obtenemos que:
por lo que los parámetros seleccionados también cumplen esta condición. Por último, podemos calcular el valor de las raíces, obteniendo:
que, como podemos comprobar, son ambas negativas y mayores que -2. En la práctica, necesitamos algún mecanismo para calcular los parámetros del modelo para una economía en particular. Estos métodos consisten en la calibración de los parámetros o en la estimación econométrica de los mismos, tal que la estructura teórica se adapte a los datos. Así, se trataría de utilizar las variables macroeconómicas para determinar algunos ratios importantes que permitan inferir el valor de los parámetros. En la actualidad, el enfoque más utilizado es la calibración de los parámetros o bien utilizar los dos métodos de forma simultánea.
Al margen de los parámetros, para que el modelo sea operacionalmente computable, también necesitamos dar valores a las variables exógenas. En primer lugar, determinamos el valor de las variables exógenas en el momento inicial, que aparecen reflejadas en la tabla 2. Estos valores son totalmente arbitrarios (aunque se podrían calibrar con datos reales), pero hemos de tener de alguna manera en cuenta el significado económico de cada variable. Estos valores nos van a permitir calcular el valor de estado estacionario para las variables endógenas.
Tabla 2. Valores de las variables exógenas
Símbolo |
Parámetros |
Valor |
β0 |
Componente autónomo de la demanda agregada |
2.100 |
m0 |
Cantidad de dinero |
100 |
yP0 |
Nivel de producción potencial |
2.000 |
Una vez hemos dado valores a los parámetros y a las variables exógenas, podemos proceder a calcular el valor inicial (estado estacionario) de las variables endógenas. En primer lugar, calcularemos el valor de estado estacionario de las dos variables endógenas de referencia, que en este caso son el nivel de precios y el nivel de producción. Para ello, igualamos a cero las dos ecuaciones dinámicas para el nivel de precios y nivel de producción y resolviendo. Si este procedimiento lo realizamos utilizando el modelo en notación matricial, resulta:
donde zt es el vector de variables exógenas y donde una barra horizontal sobre la variable denota su valor de estado estacionario. Resolviendo obtenemos las siguientes expresiones:
Por tanto, en nuestro caso resulta:
Calculando la anterior expresión obtenemos que:
Es decir, el nivel de precios de equilibrio inicial es p0=1 y el nivel de producción de equilibrio inicial es y0=2.000. Una vez obtenidos estos valores, podemos utilizar las distintas ecuaciones para calcular el resto. Así, por ejemplo, podemos utilizar la ecuación [1] para calcular el valor inicial del tipo de interés nominal. Despejando el tipo de interés nominal obtenemos que:
Sustituyendo los valores correspondientes resulta:
Por lo que el valor inicial de equilibrio del tipo de interés nominal es 2. A continuación, ya podemos calcular el valor de equilibrio inicial para la demanda agregada, sustituyendo los valores conocidos en la ecuación [2], de lo que resulta que:
Dado que si suponemos la existencia de equilibrio el nivel de precios sería constante (Δpe0 = 0), es decir yd0 = 2.000 , exactamente la misma cantidad que el nivel de producción inicial. Para comprobar finalmente que dichos valores son los correspondientes al estado estacionario podemos calcular las variaciones del nivel de precios y del nivel de producción que deberían ser cero. En efecto, si sustituimos los valores conocidos en la ecuación [3] obtendríamos:
Y finalmente, si hacemos lo mismo en la ecuación [4] el resultado sería:
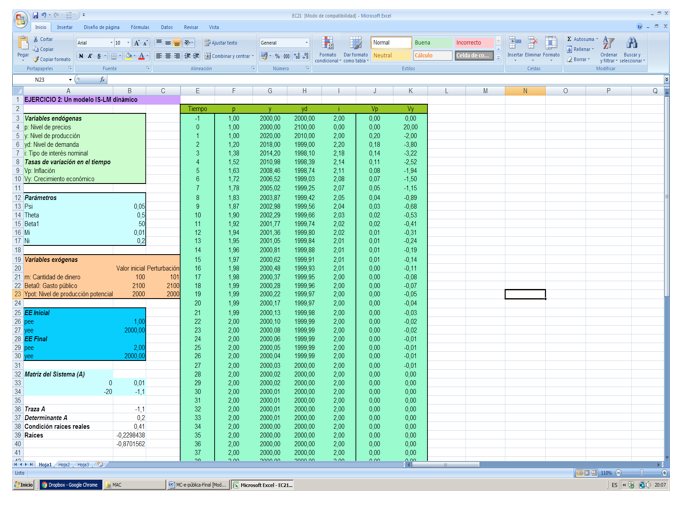
La figura 1 muestra la hoja en Excel del modelo resuelto numéricamente, donde aparecen los diferentes conjuntos de información que necesitamos: definición de las variables, determinación del valor de los parámetros, determinación del valor de las variables exógenas y cálculo del estado estacionario. A continuación aparecen los valores de cada una de las variables endógenas en cada periodo así como un gráfico de las mismas para observar su senda temporal.
Figura 1: Resolución en hoja de Excel del modelo
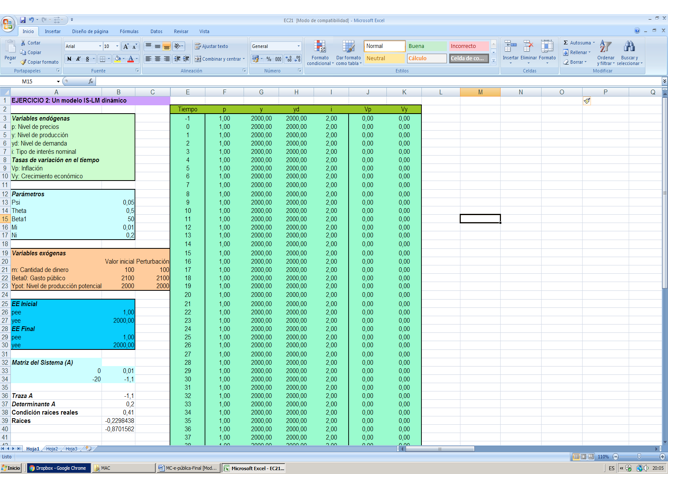
Fuente: Elaboración propia
Los valores iniciales para las variables exógenas aparecen en las celdas «B23», «B24» y «B25», que hemos denominado «Beta0», «money0» y «Ypot0», respectivamente[1]. Una vez determinados los valores de los parámetros y de las variables exógenas, a continuación procedemos a determinar el valor de las variables endógenas en el momento inicial, que lo consideramos de equilibrio, por lo que el valor de las variables endógenas coincidirá con su valor de estado estacionario. Por tanto, para calcular dicho valor, recurrimos a la definición de estado estacionario que hemos obtenido de la resolución del modelo.
Dados los valores de los parámetros y de las variables exógenas, en términos numéricos tendríamos que las dos ecuaciones en diferencias para los precios y el nivel de producción serían:
En términos matriciales el sistema resultante sería:
Las columnas «F», «G», «H» e «I» de la figura 1 muestran el valor de cada una de las variables endógenas (precios, producción, demanda agregada y tipo de interés nominal) en cada momento del tiempo. Si situamos el cursor en la celda «F3» aparece la expresión:
=(Theta*Beta0)/Beta1+money0-(Psi+Theta/Beta1)*Ypot0
Es simplemente la expresión correspondiente al valor de estado estacionario inicial del nivel de precios. Las restantes filas de esta columna simplemente contienen el valor del nivel de precios en el momento anterior más el cambio producido en dicho nivel de precios. Así, la celda «F4», contiene la expresión =F3+J3, donde «F3» hace referencia al nivel de precios del periodo anterior y «J3» al cambio en el nivel de precios. Esta expresión se copia en las restantes filas de dicha columna.
Por su parte, si situamos el cursor en la celda «G3» ésta contiene la expresión:
=Ypot0
Esto es, el valor de estado estacionario inicial del nivel de producción que se corresponde con el nivel de producción potencial. En la celda «G4», aparece la expresión =G3+K3 en la que definimos el nivel de producción de cada periodo como el anterior más el cambio experimentado en el mismo. La columna «H» contiene los valores de la demanda agregada. Si nos situamos en la celda «H3», observamos que aparece la expresión
=Beta0-Beta1*(I3-J3)
expresión que se corresponde con la ecuación de demanda agregada del modelo, en el cual la demanda agregada depende negativamente del tipo de interés real, que hemos definido como la diferencia entre el tipo de interés nominal y la inflación. Esta misma expresión aparece en las siguientes celdas de esta columna. La columna «I» contiene los valores del tipo de interés nominal. Así, la celda «I3» contiene la siguiente expresión:
=-1/Theta*(money0-F3-Psi*G3)
Es la ecuación resultante de despejar el tipo de interés de la ecuación de demanda de dinero. Si nos situamos en la celda «I4», la expresión que aparece es:
=-1/Theta*(money1-F4-Psi*G4)
Hace referencia a la nueva cantidad de dinero a partir del momento 0. Esta expresión es la misma que aparece en las siguientes filas de esta columna.
Finalmente, las columnas «J» y «K» muestran las variaciones de los precios y del nivel de producción, es decir, definen el valor de la inflación y el crecimiento de la producción en cada periodo. En este caso debemos introducir las correspondientes ecuaciones que determinan el comportamiento de ambas variables. Si nos situamos en la celda «J3» vemos que contiene la expresión:
=Mi*(G3-Ypot0)
Mientras que la celda «J4» contiene la expresión:
=Mi*(G4-Ypot1)
Siendo esta misma expresión la que aparece en las siguientes celdas, dado que es posible que queramos analizar los efectos de una alternación en el nivel de producción potencial de la economía. Por su parte, si nos situamos en la celda «K3», observamos que contiene la expresión:
=Ni*(H3-G3)
Se corresponde con la ecuación dinámica del nivel de producción. Como podemos comprobar en la hoja de cálculo podemos introducir la expresión inicial dada por el modelo, ya que también vamos a calcular en cada momento del tiempo el valor correspondiente de la demanda agregada. Si todos los cálculos son correctos, las columnas «J» e «K», donde aparece el cambio de cada variable, deben ser ceros.
4.EFECTOS DE UN AUMENTO EN LA CANTIDAD DE DINERO
Una vez resuelto numéricamente el modelo y calculado el valor de estado estacionario dados unos valores para las variables exógenas y los parámetros, a continuación vamos a utilizar dicho modelo para analizar cuáles serían los efectos sobre nuestra economía de una perturbación, esto es, un cambio en alguna de las variables exógenas. Esto nos permitirá calcular el valor de las variables endógenas en cada momento del tiempo y, por tanto, obtener la dinámica temporal de cada una de ellas. Al realizar este ejercicio en una hoja de cálculo el resultado que vamos a obtener es la respuesta temporal de cada variable ante una perturbación. Esto es lo que se denomina el análisis impulso-respuesta. En concreto, vamos a suponer que en el momento de tiempo 0 se produce un aumento en la cantidad de dinero, pasando de un valor de 100 a un valor de 101. Para realizar este ejercicio únicamente hemos de cambiar el valor de la celda «C23» y automáticamente obtendremos los resultados. Ejercicios similares podríamos realizar para estudiar el efecto de cambios en las otras dos variables exógenas: gasto público y nivel de producción potencial.
La figura 2 nos muestra el resultado en la hoja de cálculo, cuando se produce una perturbación en la economía, podemos observar que la dinámica de las variables se calcula de forma automática. Esto es así porque hemos referenciado las expresiones a partir del momento 0 respecto a los nuevos valores de las exógenas, con el objetivo de realizar análisis de perturbación. Así, en este caso concreto podemos analizar los efectos de cambios (aumentos o disminuciones) en la cantidad de dinero, cambios en el gasto público y cambios en el nivel de producción potencial. También es posible simular perturbaciones que sean combinaciones de cambios en dos o más variables exógenas de forma simultánea.
Como podemos observar, en el periodo 0 se produce una disminución instantánea del tipo de interés nominal. Así, el tipo de interés nominal pasa de 2 a ser 0. Como consecuencia de esta disminución en el tipo de interés la demanda agregada aumenta. Así pasa de un valor de 2.000 a un valor de 2.100. Este aumento de la demanda agregada va a provocar que el nivel de producción aumente en el siguiente periodo lo que a su vez provoca un aumento en el tipo de interés nominal. Por otra parte, el aumento del nivel de producción en el periodo 1 va a dar lugar a que los precios aumenten en el periodo 2. La forma más fácil de observar estos efectos es construyendo un gráfico que represente la senda temporal de cada variable a partir del momento en el cual se produce la perturbación. La figura 3 muestra las funciones impulso-respuesta de las variables endógenas ante dicha perturbación.
Figura 2: Cálculo dinámico de las variables ante un cambio en la cantidad de dinero
Fuente: Elaboración propia
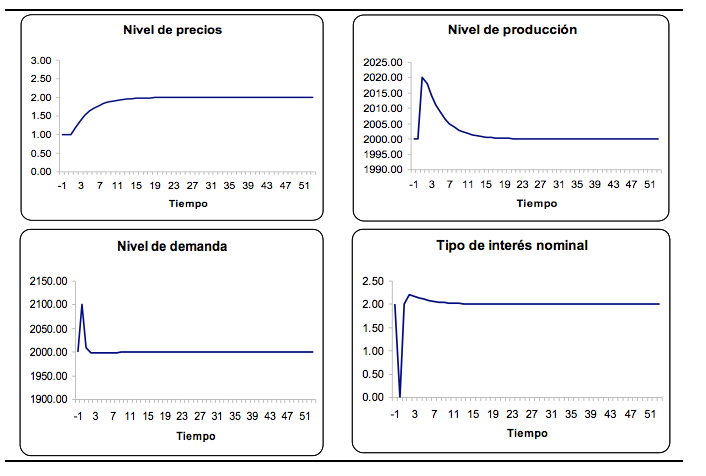
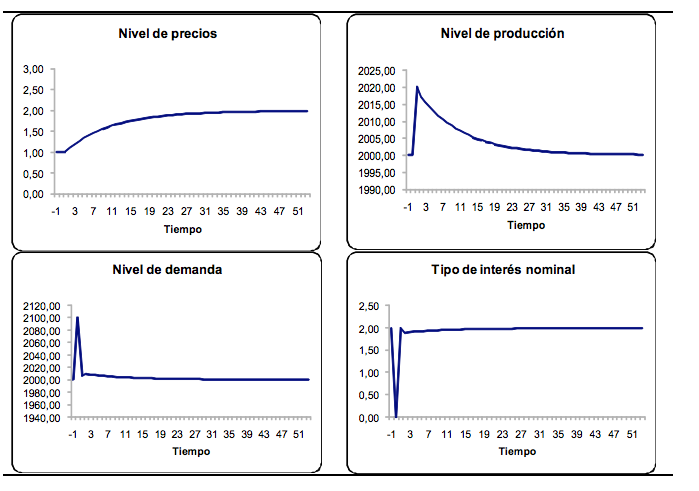
Como podemos observar en la figura 3, el nivel de precios va aumentando paulatinamente en el tiempo hasta alcanzar el nuevo estado estacionario. En este caso no se producen fluctuaciones en el nivel de precios y sigue la misma tendencia, es decir, aumenta indicando que siempre estamos en una situación de sobreproducción. Por el contrario el nivel de producción experimenta un aumento inicial para posteriormente ir disminuyendo hasta alcanzar el nuevo estado estacionario. En este caso, el nivel de producción aumenta inicialmente indicando la existencia de un exceso de demanda, pero posteriormente disminuye indicando lo contrario, esto es, un exceso de oferta. Por otra parte vemos que el ajuste inicial en el nivel de producción es muy importante, lo que significa que hemos supuesto un valor de su velocidad de ajuste que puede ser excesivamente elevado.
Por su parte, el comportamiento de la demanda agregada y del tipo de interés muestra que ambas variables tienen un elevado nivel de flexibilidad. El tipo de interés nominal es una variable flexible, que disminuye de forma instantánea ante el aumento en la cantidad de dinero. Esta disminución en el tipo de interés nominal también supone una disminución instantánea en el tipo de interés real lo que provoca a su vez un aumento en la demanda agregada. No obstante, el aumento siguiente en el nivel de producción hace que el tipo de interés nominal vuelva a aumentar, provocando el movimiento en sentido contrario en la demanda agregada.
Como podemos observar, en el largo plazo (una vez la economía ha alcanzado el nuevo estado estacionario), tanto el nivel de demanda agregada, como el nivel de producción y el tipo de interés nominal, alcanzan el mismo valor que tenían en el estado estacionario final. El único efecto que observamos en el largo plazo es un aumento en el nivel de precios. Así, el nivel de precios aumenta de un valor inicial de 1 a un valor de 2. Como podemos comprobar, este aumento en el nivel de precios es exactamente igual al aumento que se ha producido en la cantidad de dinero. Lo que nos está indicando el modelo es que se cumple el principio de neutralidad monetaria en el largo plazo. Así, estamos considerando una perturbación de carácter nominal (variación en la cantidad de dinero), que a largo plazo únicamente tiene efectos nominales (variación en el nivel de precios), sin que tenga efectos de carácter real (la producción no se ve afectada en el largo plazo).
Figura 3: Senda temporal de las variables endógenas ante una perturbación monetaria
Fuente: Elaboración propia
5. EFECTOS DE CAMBIOS EN LOS PARÁMETROS (ANÁLISIS DE SENSIBILIDAD)
Finalmente, otro de los ejercicios que podemos llevar a cabo usando la simulación numérica de nuestro modelo, es estudiar cómo responde la economía ante distintas perturbaciones en función del valor de los parámetros. A esto es lo que se denomina análisis de sensibilidad del modelo, a través de la variación de alguno de los parámetros del modelo para estudiar como la dinámica que siguen las diferentes variables se ve alterada. Por ejemplo, podríamos cambiar los parámetros de ajuste correspondientes tanto al nivel de producción como a los precios, o bien las elasticidades asociadas a la demanda de dinero con el objeto de estudiar cómo cambia la dinámica de las diferentes variables macroeconómicas ante una determinada perturbación. En el primer caso, únicamente se alteraría la dinámica de ajuste de las variables, mientras que en el segundo caso, también cambiarían los valores de estado estacionario de las variables.
En concreto, vamos a disminuir la velocidad de ajuste del nivel de producción. Así, el parámetro µ pasa de un valor de 0,01 a un valor de 0,005. De nuevo, tenemos que asegurarnos que el nuevo valor para este parámetro cumpla las propiedades descritas anteriormente. En primer lugar, la condición de que las raíces sean reales. Tal y como podemos comprobar:
En segundo lugar, se debe de cumplir adicionalmente que ambas raíces sean negativas, ya que así nos garantizamos que todas las trayectorias sean estables (en el caso en el que una raíz sea negativa pero la otra positiva, la solución sería de punto de silla), y que su valor se sitúe entre -2 y 0:
La figura 4 muestra la dinámica temporal de cada variable en este caso, que ahora son muy diferentes respecto a las obtenidas anteriormente. Tal y como podemos observar en las nuevas funciones impulso respuesta, ahora el ajuste de las diferentes variable al nuevo estado estacionario es más lento, implicando un mayor número de periodos hasta que el sistema vuelve al equilibrio. Esto es consecuencia de que hemos disminuido el parámetro de ajuste de la ecuación de inflación, que mide la velocidad a la que los precios se ajustan ante desequilibrios entre la oferta y la demanda. Al moverse los precios más lentamente hacia su nuevo valor de estado estacionario, el exceso de demanda tarda más tiempo en corregirse, por lo que también el nivel de producción se ajusta más lentamente hacia su nuevo valor de estado estacionario.
Figura 4: Senda temporal de las variables endógenas ante una perturbación monetaria (análisis de sensibilidad ante cambios en los parámetros)
Fuente: Elaboración propia
5. CONCLUSIONES
En este artículo hemos presentado uno de los ejercicios numéricos que forman parte del libro titulado Macroeconomía Computacional. Este manual comprende una serie de ejercicios de computación, usando diferentes desarrollos teóricos y que se dividen en tres partes: Modelos Dinámicos Básicos, Equilibrio General Dinámico y Crecimiento Económico. El objetivo es resolver diferentes modelos teóricos muy sencillos pero utilizando técnicas de resolución numéricas y de computación en una hoja de cálculo como Excel. A partir de la elaboración de unas sencillas hojas de cálculo es posible obtener una resolución numérica de diferentes modelos, obteniéndose las funciones impuso-respuesta ante distintas perturbaciones.
El ejercicio que presentamos en este trabajo consiste en la simulación numérica de una versión dinámica del modelo IS-LM. Para ello hemos utilizado como herramienta la hoja de cálculo Excel. En primer lugar, hemos calculado numéricamente el valor de las variables endógenas en estado estacionario, dados unos valores para los parámetros y para las variables exógenas. En segundo lugar, hemos realizado un análisis de perturbaciones, calculando las funciones impulso-respuesta de las variables macroeconómicas ante diferentes perturbaciones, que nos indican cómo cambian estas variables a lo largo del tiempo dado un cambio en alguna de las variables exógenas. Por último, este tipo de ejercicios también permiten estudiar cómo responden las variables macroeconómicas ante distintas perturbaciones en función del valor de los parámetros, o como se alteran los valores de estado estacionario de las variables endógenas. Esto es lo que se denomina análisis de sensibilidad del modelo, estudiando cómo cambian sus implicaciones en función del valor de determinados parámetros.
Notas
[1] Dar un nombre a un celda resulta un procedimiento muy adecuado si tenemos que referirnos al valor de la misma en otros cálculos y evita tener que usar los símbolos de “$” para mantener fija la referencia a dicha celda
Agradecimientos
Gracias a nuestros compañeros Benedetto Molinari y Gonzalo Fernández de Córdoba por sus comentarios respecto al material previo utilizado en la elaboración de este artículo, así como los comentarios recibidos por dos evaluadores anónimos y la co-editora ejecutiva de la revista a una versión previa del trabajo y que han resultado de gran utilidad.
REFERENCIAS
Bajo, O. y Díaz, M. C. (2011). Teoría y política macroeconómica. Antoni Bosch.
Barreto, H. (2015): “Why Excel?”, Journal of Economic Education, 46(3): 300-309.
Barreto, H. (2016): Teaching Macroeconomics with Microsoft Excel. Cambridge University Press.
Bongers, A., Gómez, T. y Torres, J. L.: (en prensa). Macroeconomía Computacional. Vernon Press.
Carlin, W. y Soskice, D. (2015):. Macroeconomics: Institutions, Instability, and the Financial System. Oxford University Press.
Del Rey, E. y Silva, J. I. (2012): “Oferta de trabajo y análisis impositivo con el ordenador: tutorial y actividad práctica”. e-pública.Revista electrónica sobre la enseñanza de la Economía Pública, 11: 1-10.
Gilbert, J. y Oladi, R. (2011): “Excel Models for International Trade Theory and Policy: An Online Resource”, Journal of Economic Education, 42 (1): 95.
Kendrick, D. M., Mercado, P. R. y Amman, H. M. (2006):. Computational Economics. Princeton University Press.
Strulik, H. (2004): “Solving Rational Expectations Models Using Excel”, Journal of Economic Education, 35(3): 269-283.