Este artículo ha recibido el premio e-pública en las X Jornadas de Docencia en Economía, celebradas en Badajoz, el 31 de mayo y 1 de junio de 2018.
1. INTRODUCCIÓN
La adopción del Espacio Europeo de Educación Superior por parte de las universidades españolas ha supuesto cambios profundos en el planteamiento del proceso de enseñanza–aprendizaje. Orientado a la adquisición de competencias y no solo de contenidos, el alumno es ahora el centro del proceso, mientras que el profesor se convierte en un guía del estudiante más que en un transmisor de conocimiento. Fomentar el aprendizaje activo, autónomo y colaborativo es su principal reto, lo que ha obligado a la revisión de las metodologías docentes utilizadas y a llevar a cabo un cuidadoso diseño de las actividades a realizar dentro y fuera del aula, así como de los correspondientes materiales. Por otra parte, la necesidad de feedback del alumno en un proceso de esta naturaleza obliga al planteamiento de una evaluación continua dinámica que proporcione rápidamente al estudiante información acerca de su desempeño.
En esta línea, un grupo de profesores de estadística de la Facultad de Economía y Empresa de la Universidad de Murcia hemos diseñado una serie de aplicaciones interactivas con objeto de orientar el aprendizaje autónomo de nuestro alumnado. Por una parte, se ha creado un primer conjunto de aplicaciones que se han incorporado a la actividad docente diaria, con las que los estudiantes pueden experimentar para mejorar su comprensión de nociones y técnicas que les suelen resultar complicadas. Por otra, en un intento de dirigir y reforzar el aprendizaje, se han diseñado también un segundo conjunto de aplicaciones de evaluación que permiten medir el grado de consecución de conocimientos y competencias tanto al propio estudiante como al profesor.
Algunas de las aplicaciones del primero de los dos grupos pueden ser usadas en diferentes materias, durante las clases teóricas y prácticas. Con ellas se trabaja online para clarificar conceptos y técnicas. Como ejemplo, la aplicación https://mcuant.shinyapps.io/gr_deficit/ que permite visualizar datos de series temporales relativos al déficit de las comunidades autónomas, y puede ser utilizada tanto en asignaturas de Estadística como de Economía del Sector Público. O la aplicación https://mcuant.shinyapps.io/gr_educacion/ que trabaja con representaciones gráficas de datos, en este caso de gasto público per cápita en educación a nivel regional, y puede ser de interés en las asignaturas anteriormente mencionadas y en Economía Mundial o Economía de la Educación. Finalmente, la aplicación https://mcuant.shinyapps.io/gr_deuda/ que visualiza datos de deuda pública en las comunidades autónomas e incorpora una pestaña de autoevaluación sobre las diferentes tasas de variación que se pueden construir, con indicaciones sobre la forma adecuada de obtener la solución.
Aunque el uso de recursos interactivos es cada vez más habitual en las universidades españolas, en general estos recursos no suelen presentar comentarios individualizados relativos al progreso experimentado por cada estudiante, ni tampoco están diseñados para promover el aprendizaje colaborativo (Del Moral y Villalustre, 2012). Las aplicaciones interactivas de evaluación que constituyen el segundo grupo anteriormente descrito, buscan avanzar en ese sentido, ya que se han planteado como instrumentos que posibilitan la autoevaluación por parte del alumno de su propio progreso en el aprendizaje a la vez que fomentan la colaboración entre los estudiantes.
Estas actividades de autoevaluación forman parte de la evaluación continua de nuestras asignaturas, con un peso específico en la calificación final, para así incentivar su uso. Pensamos que ello debe ser así porque los estudios empíricos sugieren que la participación en actividades de autoevaluación resulta motivadora para los estudiantes, mejorando su aprendizaje y sus resultados (Dinov et al., 2008; Ibabe y Jauregizar, 2010; Romeu et al., 2016).
Puesto que buena parte de las prácticas de nuestras asignaturas de estadística se abordan con el paquete R, a través de la interfaz RStudio, se ha usado también este software para el diseño de las aplicaciones interactivas. R es un entorno y lenguaje de programación enfocado al análisis de datos, muy usado en investigación y cada vez más también en docencia. Permite un mayor control sobre el análisis que los paquetes estadísticos tradicionales, facilitando la investigación reproducible, y posibilita abordar un estudio de forma completa, incluyendo herramientas tanto para la depuración de datos como para la presentación de resultados. Una de sus principales ventajas es que se trata de software libre, continuamente actualizado y completado con nuevos paquetes accesibles desde el repositorio CRAN de la web del Proyecto R (https://cran.r-project.org/), o también desde la plataforma de desarrollo colaborativo GitHub (https://github.com/github). Los usuarios de R conforman una comunidad colaborativa muy activa, que comparte no solo código sino también materiales que facilitan el uso de los distintos paquetes, lo que ha sido determinante para la generalización de su uso en los últimos años (Muñoz, 2013).
En particular, el repositorio CRAN incluye el paquete Shiny para la creación de páginas webs interactivas (https://shiny.rstudio.com). Esta nueva herramienta, ampliamente utilizada para presentación y visualización de resultados de análisis de datos reales, también se puede aprovechar en enseñanza para profundizar en la comprensión de conceptos y técnicas, en particular de naturaleza estadística (Arias et al, 2016; Gómez et al., 2016; Mulero, 2017). Además, su capacidad para generar exámenes personalizados es muy útil para plantear pruebas de autoevaluación (Ferre et al., 2017).
En esta última línea, hemos utilizado Shiny para desarrollar todas las aplicaciones web interactivas, incluidas las de autoevaluación que permiten al estudiante gestionar y valorar su aprendizaje. En cada una de ellas, a partir de una estructura común se generan actividades individualizadas usando el número de DNI de cada alumno. Su estructura común permite que los estudiantes trabajen de forma colaborativa al utilizar las aplicaciones. Por otra parte, la individualización de los datos y/o las actividades a realizar por cada estudiante hacen que este tenga que resolver sus propios ejercicios, lo que requiere de su trabajo y aprendizaje autónomo. Las aplicaciones han sido programadas para que el profesor pueda verificar con facilidad si el estudiante ha completado correctamente sus actividades, facilitando así su calificación. Esto último permite realizar actividades de evaluación continua incluso con grupos muy numerosos.
Todas estas aplicaciones son accesibles online empleando cualquier navegador estándar y desde gran variedad de dispositivos, resultando muy adecuadas para el trabajo no presencial. Cada respuesta del alumno se evalúa automáticamente in situ en el navegador, y el resultado se le comunica de manera inmediata. De esta forma, recibe un feedback continuo sobre su progreso, tanto cuando las respuestas son correctas (con explicaciones o comentarios sobre posibles alternativas) como cuando son erróneas (con indicaciones para redirigir su aprendizaje).
Las aplicaciones requieren estar alojadas en un servidor especial, que mantiene activo un proceso subyacente basado en R, encargado de personalizar el ejercicio de cada estudiante, evaluar las respuestas conforme se van introduciendo y mantener actualizado el registro de alumnos que han resuelto cada ejercicio, entre otras tareas. De momento, hemos optado por el uso del servidor comercial que provee la plataforma shinyapps.io (http://www.shinyapps.io/), aunque estamos trabajando en la consecución de un servidor propio.
El resto del artículo se organiza de la siguiente manera. En la sección 2 se describen, junto a la metodología empleada para introducir las aplicaciones Shiny en nuestra docencia, la estructura de estas. La sección 3 está dedicada a presentar los resultados derivados del uso de estas aplicaciones de acuerdo a dicha metodología. Por último, las conclusiones y algunas líneas futuras de actuación se recogen en la sección 4.
2. METODOLOGÍA
Como parte del Proyecto de Innovación Docente de la Universidad de Murcia “Ejercicios on-line interactivos de Estadística con Shiny” se han elaborado varias aplicaciones interactivas online que cubren diferentes aspectos de los tres bloques en los que tradicionalmente se organiza la docencia en estadística: estadística descriptiva, probabilidad e inferencia estadística (Pérez et al., 2017). Se describe a continuación el uso de estas aplicaciones en una asignatura concreta, “Estadística aplicada a la Empresa II”, que es la primera en la que empezamos a integrarlas. Son muchas las aplicaciones elaboradas en el contexto de la asignatura y son varios los fines a los que están orientadas, pero en este trabajo se tratarán únicamente aquellas relacionadas con autoevaluación. Se aportarán, incluso, enlaces a algunas de ellas para facilitar el examen de su contenido, estructura y funcionalidad.
La asignatura de “Estadística aplicada a la Empresa II” se ubica en segundo curso del grado en Administración y Dirección de Empresas de la Universidad de Murcia. La experiencia descrita en este trabajo se ha llevado a cabo en el primer cuatrimestre del curso 2017-18. De los 471 estudiantes matriculados, organizados en 7 grupos, un total de 373 pertenecían a los 5 grupos en los que impartían clase profesores de nuestro grupo de trabajo.
Esta asignatura está dedicada principalmente a la Inferencia Estadística, y se compone de los siguientes temas:
Tema 1. Modelos de variables aleatorias
Tema 2. Introducción a la Inferencia Estadística
Tema 3. Estimación puntual
Tema 4. Intervalos de confianza
Tema 5. Contrastes de hipótesis
Para cada uno de estos temas se trabajan actividades prácticas con R y RStudio en el aula de informática. El material docente empleado se elaboró en el marco de un Proyecto de Innovación Docente anterior y ha sido publicado como OpenCourseWare de la Universidad de Murcia (Molera et al., 2017). Entre los recursos disponibles pueden encontrarse prácticas resueltas para cada uno de los temas, prácticas propuestas y distintos materiales de experimentación y autoaprendizaje elaborados tanto con el propio R como con Geogebra. Todas estas herramientas se integran en el desarrollo de las clases.
La evaluación de la asignatura es común a todos los grupos y consta de cuatro herramientas:
- a) Exámenes intermedios (15% de la nota final).
- b) Análisis de datos con R (10% de la nota final).
- c) Carpeta de actividades (5% de la nota final).
- d) Examen final (70% de la nota final).
Es en el apartado de la carpeta de actividades donde se integran las actividades de autoevaluación. En concreto, después de que cada práctica sea trabajada en clase, los estudiantes disponen habitualmente de una semana para completar una o varias actividades de autoevaluación de los contenidos y habilidades desarrolladas.
2.1. Estructura de las aplicaciones Shiny
Las aplicaciones interactivas de autoevaluación se han elaborado con el paquete Shiny de R, a veces combinado con R Markdown (https://rmarkdown.rstudio.com/). Ello ha permitido dotarlas de formatos variados, entre los que destacamos el formato de diapositivas y el de textos interactivos extensos. Puesto que, en última instancia, el lenguaje con el que se confeccionan estos materiales es lenguaje HTML, se han podido emplear también recursos propios de dicho lenguaje, tales como el código CSS, para dotar a los materiales del aspecto final deseado por cada profesor. Esta variedad de formatos es muy útil, ya que las aplicaciones pueden adaptarse a las necesidades específicas de cada situación. Además, posibilita que las experiencias en el aula sean variadas, lo que es una fuente adicional de motivación para algunos estudiantes.
Como ejemplo, describimos a continuación una de las aplicaciones desarrolladas, disponible en https://feeumu.shinyapps.io/IntervalosConfianza/, que se corresponde con una página web continua con preguntas interactivas incrustadas que incluyen múltiples comentarios compuestos de texto, ecuaciones y figuras. En ella, se guía al estudiante para que realice, paso a paso, ejercicios de intervalos de confianza para una población normal. Ejemplos de aplicaciones similares en el contexto de los contrastes de hipótesis o de las distintas técnicas de estimación se pueden encontrar en las direcciones siguientes: https://feeumu.shinyapps.io/Contrastes/ y https://feeumu.shinyapps.io/Inferencia/.
Dado que uno de los objetivos de esta metodología es ofrecer una experiencia de aprendizaje personalizada a los estudiantes, en primer lugar, la aplicación solicita la identificación del usuario mediante su DNI (Figura 1). Este se emplea como parte de una semilla aleatoria en la codificación de los ejercicios, lo que permite que tanto los datos a usar como las propias preguntas puedan ser distintos para cada estudiante. Sin embargo, la estructura general de la actividad es la misma para todos, lo que favorece la resolución colaborativa de los ejercicios.
Figura 1. Instrucciones de uso de la aplicación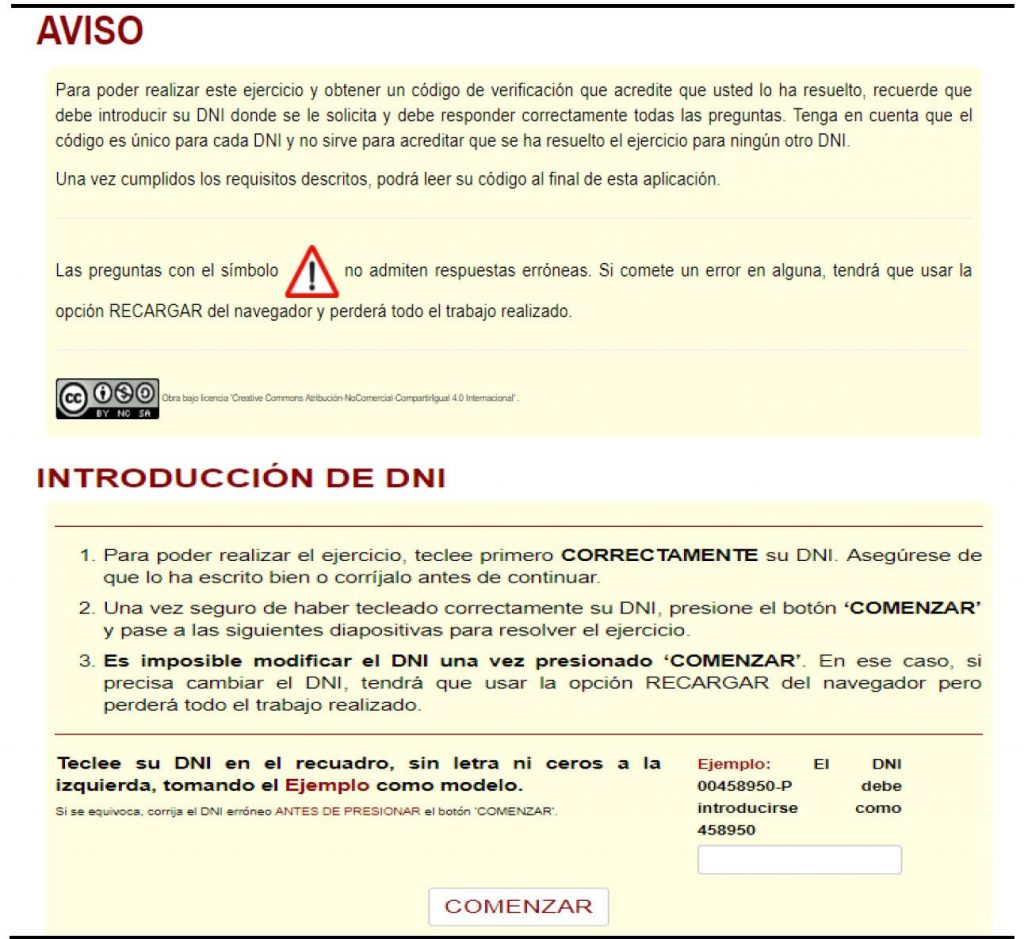
En la Figura 2 se puede apreciar cómo, aun refiriéndose a los mismos conceptos y técnicas (intervalos de confianza en poblaciones normales, en este caso), las características específicas de una pregunta y el conjunto de datos descargado por cada estudiante son diferentes al estar personalizados a partir del DNI. Obviamente, las soluciones de los ejercicios también son diferentes, y no sólo numéricamente, sino también en términos de sus conclusiones cualitativas finales.
Figura 2. Mismo ejercicio personalizado a partir de dos DNIs diferentes
En el caso de preguntas de opción múltiple, se añadió un mecanismo sencillo que dificulta la búsqueda de la respuesta correcta mediante el método de prueba y error. Si la respuesta es incorrecta, la aplicación se bloquea y obliga a comenzar de nuevo su ejecución. Tras el reinicio, las tareas a realizar y sus soluciones siguen siendo las mismas para cada alumno, pero este se ve obligado a efectuar el incómodo proceso de introducir de nuevo los resultados de las cuestiones que ya había resuelto correctamente. Las preguntas dotadas de esta característica están señaladas con un símbolo al efecto (Figura 3) y su existencia ha sido una de las principales quejas de los alumnos. Sin embargo, creemos que deben mantenerse puesto que les obligan a pensar con más cuidado las respuestas.
Las cuestiones incluidas en las aplicaciones pueden programarse de muchas maneras diferentes. En la aplicación que se examina aquí como ejemplo, decidimos usar, principalmente, dos tipos: preguntas de opción múltiple, con una posible respuesta correcta, y preguntas numéricas, cuyas respuestas deben introducirse en forma de una cantidad con un cierto nivel de precisión.
Figura 3. Ejemplo de cuestiones de opción múltiple
Para mejorar la experiencia de aprendizaje, se han incluido muchos comentarios que se muestran tanto cuando se introducen respuestas correctas como incorrectas. En el primer caso, por ejemplo, pueden generarse nuevas cuestiones o que planteen reflexiones sobre resoluciones o interpretaciones alternativas de los resultados. En el segundo, los comentarios tratan de ayudar a los alumnos a conseguir la solución correcta dependiendo del error que hayan cometido (Figura 3).
En las preguntas numéricas, si el resultado introducido es erróneo, el estudiante puede intentarlo una y otra vez hasta que obtenga la solución correcta (Figura 4). En este caso, la aplicación, ante errores en la respuesta, proporciona comentarios apropiados para reconducir la forma de obtener el valor o valores solicitados.
Figura 4. Ejemplo de cuestión numérica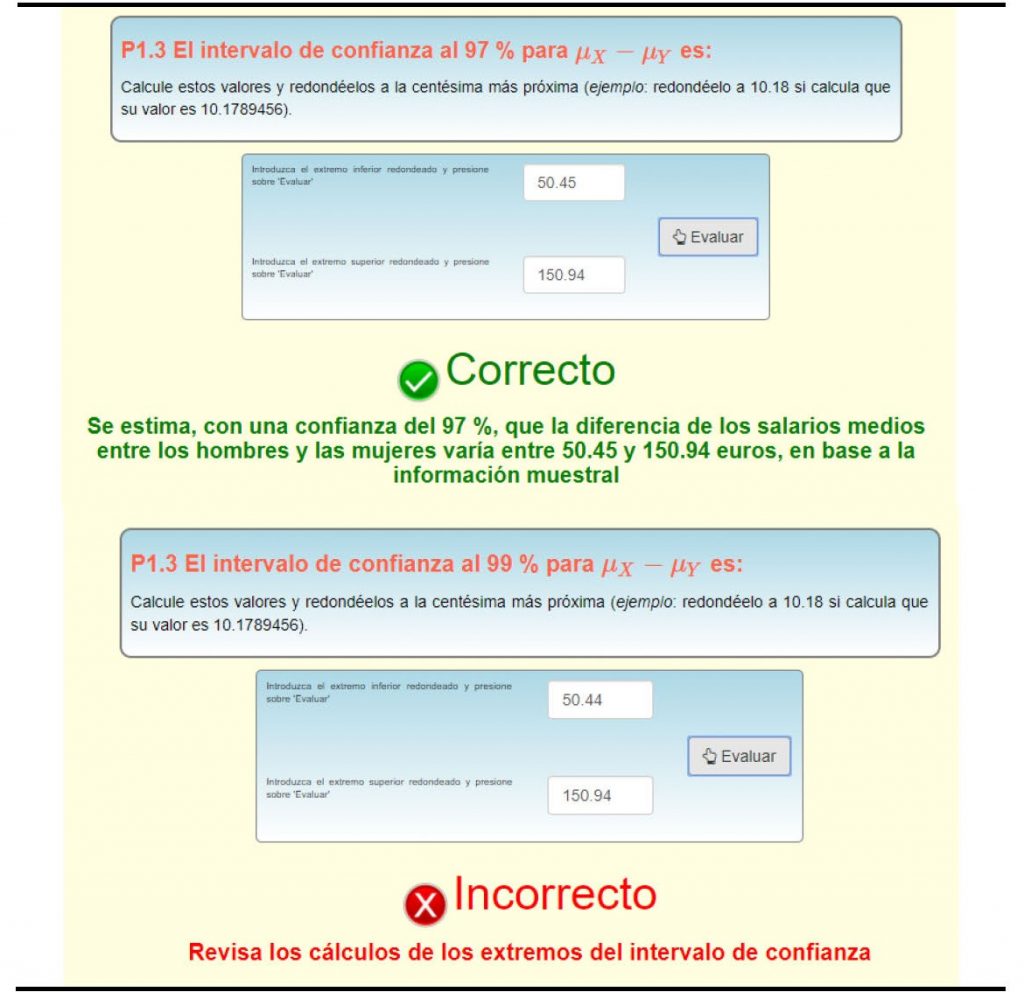
Una vez que todas las preguntas son contestadas correctamente, los estudiantes reciben un código de verificación personal que prueba que han resuelto con éxito la actividad de autoevaluación (Figura 5). Aunque se solicita a los estudiantes que envíen a su profesor el código de verificación y el script con las órdenes en lenguaje R empleadas en la resolución de la actividad, las aplicaciones están programadas para que los códigos se registren de forma automática en una cuenta de Dropbox (https://www.dropbox.com/), de modo que el profesor puede controlar cómodamente la realización de estas actividades. Las condiciones para llegar al código de verificación son también una de las principales quejas de los alumnos, ya que sólo se obtiene cuando todos los ejercicios de la actividad han sido resueltos correctamente. No obstante, a este respecto hay que precisar que los estudiantes pueden preguntar cualquier duda sobre los ejercicios durante su período de resolución, que dura varios días, tanto al profesor como a sus propios compañeros. Incluso se abren foros online al respecto en la plataforma virtual de la asignatura.
Figura 5. Código de verificación personal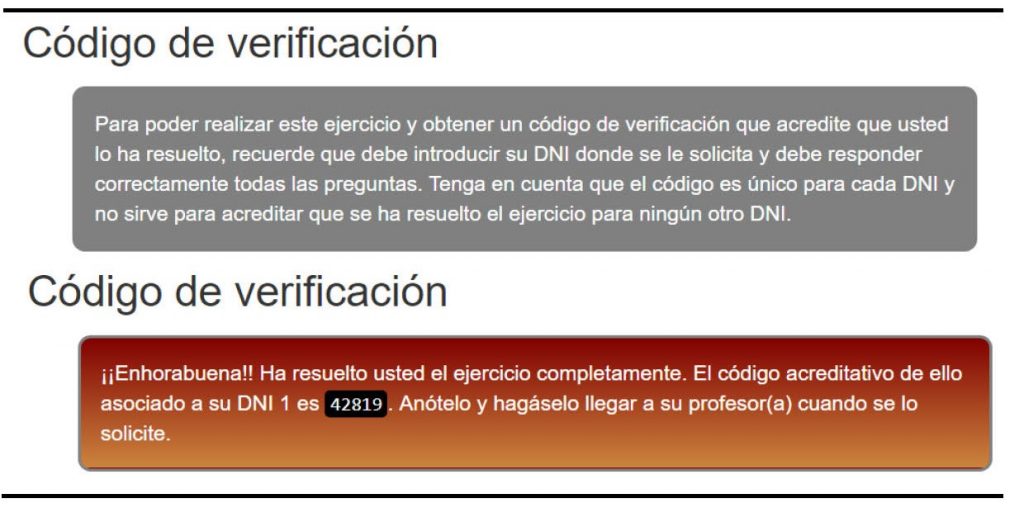
Adicionalmente, se emplean también los recursos de Google Analytics (https://analytics.google.com/) para monitorizar y obtener datos anónimos sobre el uso de las aplicaciones. Ello permite, por ejemplo, obtener estadísticas sobre la evolución en el tiempo de su frecuencia de utilización durante el periodo habilitado para su resolución.
3. RESULTADOS
En esta experiencia han participado cinco de los siete grupos en los que se encuentran divididos los alumnos de la asignatura, correspondientes a tres profesores (denotados en adelante como A, B y C) que tienen docencia en ella y, a la vez, participaban en el proyecto anteriormente mencionado. Los cinco grupos reunían un total de 373 alumnos. Para evaluar la experiencia, se dispone de los datos de una encuesta de satisfacción con las aplicaciones de autoevaluación, dirigida al alumnado (ver el contenido del cuestionario en el Anexo), así como del porcentaje de actividades entregadas y de las calificaciones obtenidas por los alumnos en la parte práctica de la prueba final de la convocatoria ordinaria de febrero de 2018, que había que resolver con R. A efectos comparativos, también se recopiló esta información (porcentaje de actividades y calificación) para el curso anterior.
3.1. Encuesta de satisfacción con las actividades de autoevaluación
Esta encuesta se llevó a cabo al final del cuatrimestre, durante una de las actividades de evaluación continua de la asignatura, en concreto en la denominada “Análisis de datos con R”. La encuesta fue contestada por 227 estudiantes, lo que supone un 93% de los que realizaron esa actividad. Aproximadamente la mitad son alumnos de primera matrícula, y el porcentaje de mujeres es ligeramente inferior al de hombres. Los estudiantes se reparten en proporciones similares entre los grupos, pero a los profesores A y C, por ser responsables de dos grupos cada uno, les corresponde un mayor número de alumnos. Esta información puede ampliarse en el gráfico de mosaico de la Figura 6.
Figura 6. Distribución de los estudiantes según profesor, género y tipo de matrícula
La valoración de las aplicaciones interactivas en la encuesta resultó muy positiva. Un 96% de los estudiantes las encontró útiles para la comprensión de los conceptos más complicados. La valoración media (en una escala de 0 a 10) fue de 7.14, y al menos el 50% les dio una puntuación mayor o igual a 7. Los gráficos boxplot o diagramas de caja de la Figura 7 sirven para detectar posibles diferencias entre las valoraciones por profesor, género y tipo de matrícula, así como desviaciones de la normalidad (asimetría y valores extremos).
Aunque, en general, no se admite la normalidad de los datos, como las muestras no son pequeñas y el test de Levene no rechaza la hipótesis de homocedasticidad (p-valores de 0.2483, 0.6409 y 0.2366 para profesor, género y matrícula, respectivamente), se lleva a cabo una prueba F de Análisis de la Varianza (ANOVA) para comparar la valoración media de las actividades por profesor, y sendas pruebas t de Student (t-test) para la comparación por género y tipo de matrícula. Ninguna de ellas muestra que dicha valoración pueda considerarse diferente según estas características.
Figura 7. Valoración de las actividades de autoevaluación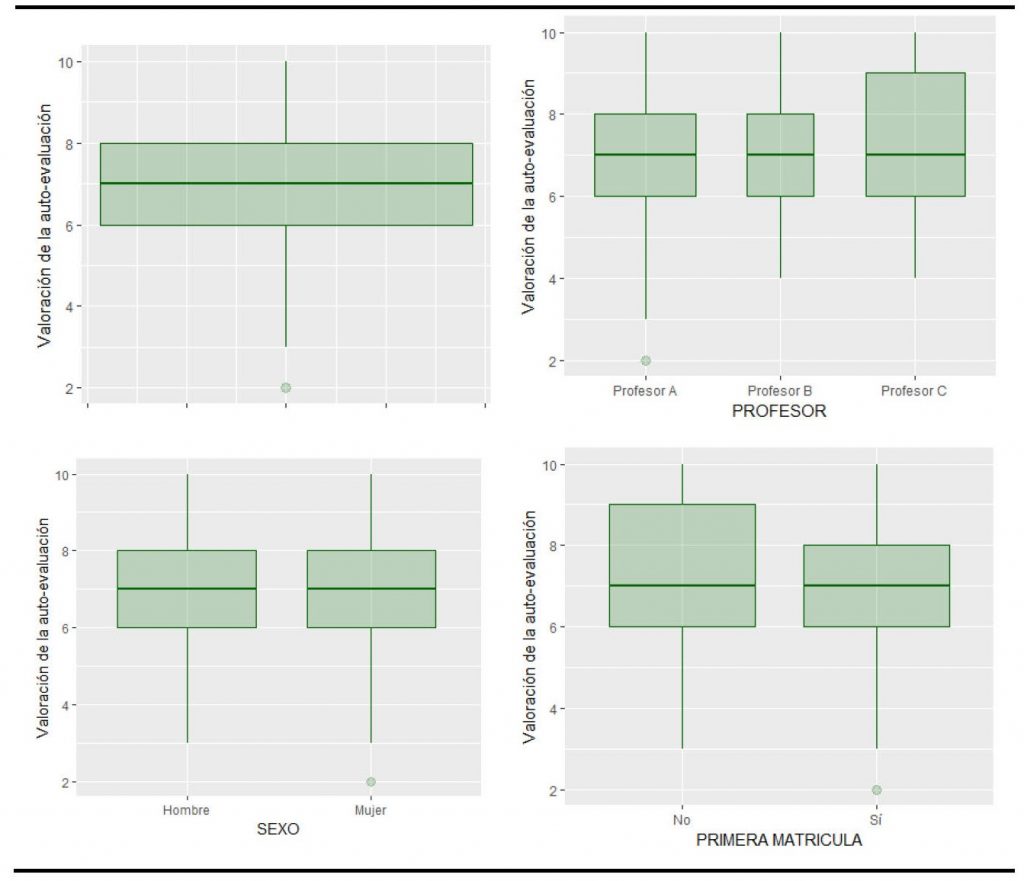
Si bien tradicionalmente la alternativa para el ANOVA cuando no se cumplían sus supuestos eran los contrastes no paramétricos (Mann-Whitney para dos muestras y Kruskal-Wallis para tres o más), actualmente, para distribuciones que difieren en simetría o presentan valores extremos, se recomiendan contrastes basados en medidas robustas, como la media recortada (Wilcox, 2012). En particular, se dispone del contraste de Yuen-Welch (Yuen, 1974) con distribución t aproximada para el caso de dos grupos y de un contraste tipo Welch con distribución F aproximada para el caso de más de dos grupos, así como de sus versiones bootstrap, implementados todos ellos en el paquete WRS2 (Mair y Wilcox, 2016) de R. Tampoco se detectan con ellos, en ningún caso, diferencias significativas entre los parámetros robustos de localización considerando el profesor, el género o el tipo de matrícula del estudiante (Tabla 1).
Tabla 1. Contrastes para la valoración de las actividades de autoevaluación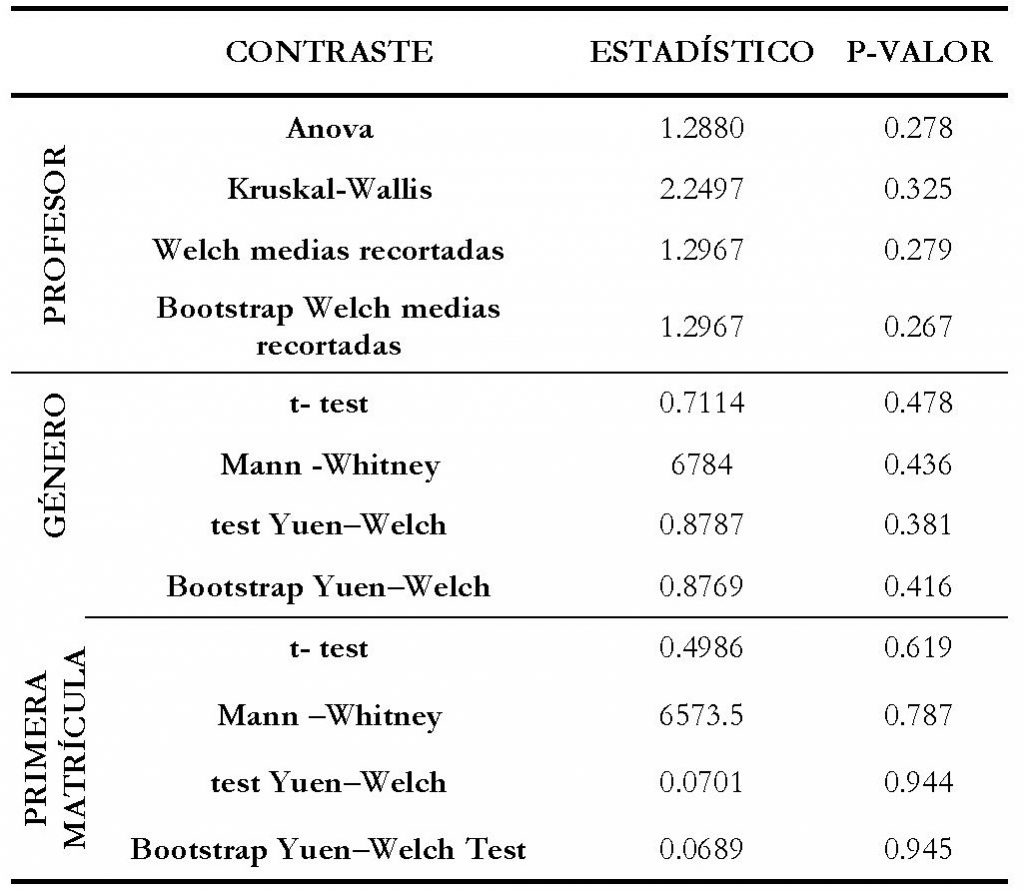
3.2. Análisis del efecto de las aplicaciones en la evaluación de la asignatura
Para analizar el efecto de las aplicaciones de autoevaluación se dispone de información relativa al alumnado del que fueron responsables los tres profesores que participan en la experiencia tanto en este curso académico (2017-18), como en el anterior (2016-17). En 2016-17 las actividades de autoevaluación de las prácticas no empleaban aplicaciones interactivas, sino que estaban basadas en una batería de ejercicios comunes a todos los alumnos, que debían entregar en distintas fechas a través de la plataforma virtual. En ese curso los tres profesores impartían clase en seis grupos, con un total de 442 estudiantes, de los cuales 208 se presentaron a la prueba final en la convocatoria ordinaria de febrero. El estudio se centra en los resultados de esa convocatoria porque es la única con información disponible para el curso 2017-18 en el momento de la redacción de este documento. A la prueba final de la convocatoria de febrero de este otro curso, se presentaron 149 alumnos de los grupos de los tres profesores considerados.
En la Figura 8 se recogen las características de los estudiantes presentados en la convocatoria de febrero en cada uno de los cursos. Se puede observar que, mientras que el porcentaje de hombres y mujeres es similar en ambos cursos, el de estudiantes de primera matrícula es superior al resto, aunque la diferencia entre ambos porcentajes es menor en 2017-18 (53.02% frente a 46.98%) que en 2016-17 (65.38% frente a 34.62%).
Figura 8. Distribución de presentados según profesor, género y tipo de matrícula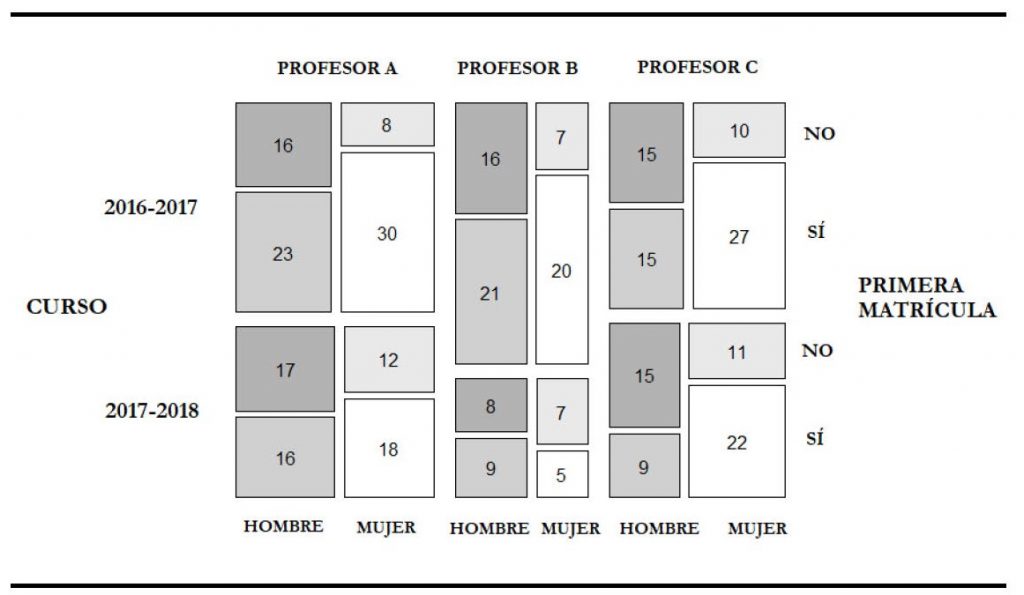
En el curso 2016-17, la carpeta de actividades relacionadas con el uso de R estaba constituida por ejercicios a entregar que eran comunes a todos los alumnos. Además, no era necesario completarlos correctamente en su totalidad. En muchos casos, los estudiantes entregaban los ejercicios con algunos errores y, a veces, se copiaban la resolución unos de otros. El uso de las aplicaciones interactivas en el curso 2017-18 y el diseño empleado en las mismas, aleatorio e individualizado, ha obligado a los alumnos a trabajar más y mejor. El porcentaje de seguimiento tiene ahora mucho más valor, ya que refleja el porcentaje de actividades realizadas correcta e individualmente por cada alumno.
En la Figura 9 se observa que, en ambos cursos, el 50% de presentados en la convocatoria ordinaria ha realizado más del 80% de las actividades propuestas. El seguimiento medio en el curso 2016-17 fue del 68.65% y en el curso 2017-18 del 78.71%, lo que supone un incremento de 10 puntos porcentuales. Ambos valores se representan sobre los diagramas de caja en forma de líneas discontinuas.
Los datos sugieren que, a pesar de que con la introducción de las aplicaciones interactivas es más complicado para un estudiante alcanzar un determinado porcentaje de actividades entregadas, el seguimiento de la carpeta de actividades no solo no disminuye, sino que aumenta.
El objetivo principal es estudiar el efecto del uso de las aplicaciones interactivas de autoevaluación en los resultados de nuestros alumnos. Para ello analizamos las calificaciones obtenidas por los estudiantes en la parte práctica del examen final de la convocatoria ordinaria de febrero, que se realiza en el aula de informática con R. En los dos cursos estudiados, la materia no cambió, el examen fue muy similar y también los criterios empleados en su corrección. La principal diferencia e innovación realizada en el curso 2017-18 fue la introducción de las aplicaciones de autoevaluación interactivas, diseñadas para favorecer el aprendizaje autónomo de los estudiantes y mejorar sus destrezas y competencias en el análisis de datos con el uso del paquete estadístico R. En concreto, la hipótesis a contrastar es:
“Las calificaciones en la prueba práctica realizada con R en el examen final son superiores cuando se emplean estas aplicaciones en las actividades de autoevaluación”.
Figura 9. Porcentaje de seguimiento de las actividades prácticas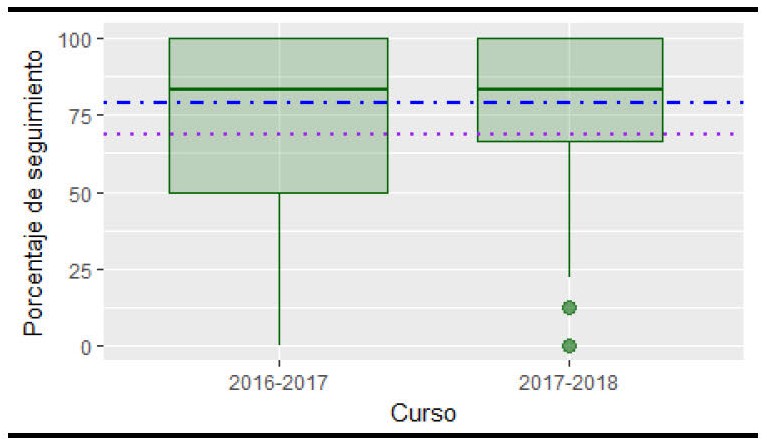
Las calificaciones obtenidas este curso (2017-18) son claramente superiores a las del curso pasado (Figura 10), con una nota media de 5.55 frente a los 3.86 puntos de 2016-17. Las distribuciones son ligeramente asimétricas, una a la derecha (2016-17) y otra a la izquierda (2017-18), con curtosis negativa. La variabilidad de las notas en ambos cursos es similar.
Figura 10. Calificación en la parte práctica del examen final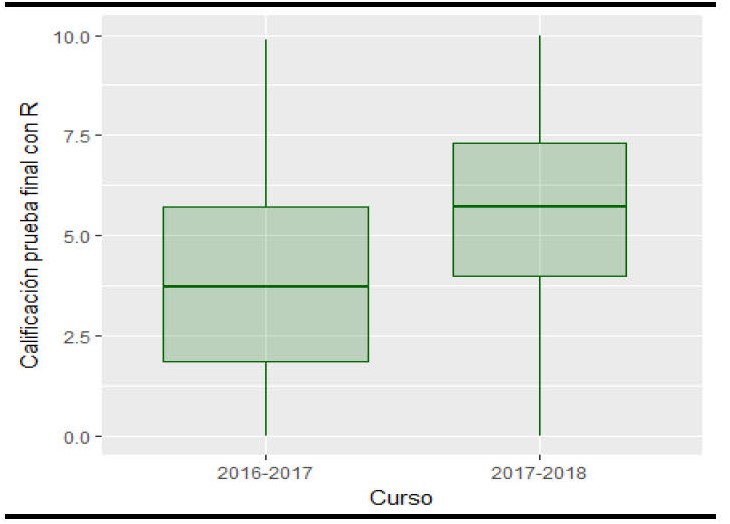
En la Tabla 2 se presentan los resultados de comparación de medias mediante un ANOVA de cuatro factores (para eliminar el efecto de la variabilidad debido al profesor, el género o el ser o no de primera matrícula) con corrección de heterocedasticidad al detectarse diferencias en variabilidad. Para realizar este contraste se ha utilizado el paquete car (Fox y Weisberg, 2018) de R. Como podemos observar, la diferencia de las notas medias en la prueba final de los dos cursos es significativa y, teniendo en cuenta los valores muestrales, podemos concluir que las calificaciones obtenidas por los estudiantes en la parte práctica del examen final son significativamente superiores cuando la carpeta de actividades la componen aplicaciones interactivas de autoevaluación. Esto apoya nuestra tesis de que estas actividades han contribuido a mejorar la comprensión de los conceptos estadísticos estudiados y su tratamiento con el software estadístico R.
Tabla 2. Contraste para las calificaciones en la parte práctica del examen final
4. CONCLUSIONES
En los últimos años se ha incorporado el uso del software R y de la interfaz RStudio a la docencia de las asignaturas de estadística del Grado en Administración y Dirección de Empresas de la Universidad de Murcia. R es una herramienta muy potente para el procesamiento, manipulación y análisis de datos, y la interfaz RStudio facilita su uso. Entre sus complementos, el paquete Shiny posibilita la creación de aplicaciones interactivas, que permiten afrontar el aprendizaje de la estadística desde una perspectiva diferente, más atractiva y motivadora. En particular, las aplicaciones diseñadas para autoevaluación durante el curso 2017-18 se han revelado como una herramienta eficaz para aumentar la implicación de los estudiantes en la asignatura y mejorar sus resultados.
La experiencia ha sido muy positiva, tanto desde el punto de vista del profesorado como del alumnado. Los docentes hemos percibido una mejora en el manejo autónomo del paquete R por parte de los estudiantes, así como una mayor comprensión de conceptos y métodos estadísticos. La aceptación entre los alumnos ha sido alta, como muestra la encuesta anónima realizada al final del cuatrimestre. Los estudiantes sostienen que el uso de estas aplicaciones les ha ayudado a entender mejor las nociones y técnicas estadísticas estudiadas. Además, destacan la facilidad de uso y el hecho de haber podido practicar con más ejercicios.
Junto a la percepción positiva de estas aplicaciones interactivas, hemos observado que los alumnos que usan estas aplicaciones realizan un mayor porcentaje de trabajos en la carpeta de actividades, y esto se traduce también, posteriormente, en mejores calificaciones finales.
Dado el éxito de esta experiencia, nos planteamos, por un lado, cambiar las ponderaciones de los instrumentos de evaluación para que la carpeta de actividades tenga mayor peso en la evaluación final de la asignatura y, por otro, promover la extensión de esta metodología a otras materias, como Economía Pública o Economía Aplicada, para las que ya se dispone de algunas aplicaciones que se podrían transformar fácilmente en autoevaluaciones personalizadas.
Hay que destacar que esta metodología garantiza que el trabajo autónomo del alumno realmente lo es, ya que cada estudiante se enfrenta a ejercicios individualizados, con una estructura común, que debe resolver de forma exitosa. Además, el emplear estas aplicaciones de evaluación interactivas en la docencia no supone una carga adicional para el profesor, pues incluyen, en su diseño, la corrección automática de las tareas propuestas y el control también automático de su resolución efectiva. Esto último supone una ventaja sustancial cuando los grupos son numerosos.
ANEXO
Preguntas en el cuestionario a estudiantes
Referencias
Arias, J., Giraldo, M., Montoya, V., Montoya, L., Usuga, O., Hernández, F. (2016): “Aplicación en Shiny para distribuciones muestrales”, XXVI Simposio Internacional de Estadística, Sincelejo, Sucre, Colombia.
Dinov, I.D., Sánchez, J., Christou, N. (2008): “Pedagogical utilization and assessment of the statistic online computational resource in introductory probability and statistics courses”, Computers & Education 50: 284-300.
Del Moral Pérez, M.E., Villalustre Martínez, L. (2012): “University teaching in the 2.0 era: virtual campus teaching competencies”, Revista de Universidad y Sociedad del Conocimiento 9 (1): 231-244.
Ferre Jaén, E., Río Alonso, L., Maurandi López, A. (2017): “ExamRandomizeR: Una aplicación web para la generación de exámenes aleatorizados que faciliten situar el Examen como herramienta de aprendizaje y no solo de evaluación en el aula de matemáticas”, Congreso IN-RED.
Fox, J. y Weisberg, S. (2018): “car: Companion to Applied Regression”, https://cran.r-project.org/package=car.
Gómez, D.S., Molina, M.D., Mulero, J., Nueda, M.J., Pascual, A. (2016): “Aplicaciones diseñadas con Shiny: un recurso docente para la enseñanza de la estadística”, XIV Jornadas de redes de Investigación en Docencia Universitaria, Alicante.
Ibabe, I., Jauregizar, J. (2010): “Online self-assessment with feedback and metacognitive knowledge”, Higher Education 59 (2): 243-258.
Mair, P. y Wilcox, R. (2016): “WRS2: A Collection of Robust Statistical Methods”, https://CRAN.R-project.org/package=WRS2.
Molera, L., Arnaldos, F, Díaz, M.T., Faura, U., Parra, I. (2017): “Curso práctico de Inferencia Estadística con R». https://www.um.es/web/innovacion/educacion-abierta/cursos/curso-practico-de-inferencia-estadistica-con-r-2016
Mulero, J. (2017): “Taller de aplicaciones estadísticas con Shiny: ShinyEst”, VIII Jornadas de Enseñanza y Aprendizaje de Estadística y la Investigación Operativa, Girona.
Muñoz Márquez, M. (2013): “Proyecto R-UCA: Pasado, presente y futuro. Desarrollo de aplicaciones con R y Shiny. IV Jornadas para la Enseñanza y Aprendizaje de la Estadística y de la Investigación Operativa, Cádiz.
Pérez, J. J., Arnaldos, F., Díaz, M. T., Faura, U. y Molera, L. (2017): “Shiny como herramienta de aprendizaje y evaluación en Estadística para la Empresa”. IX Jornadas de Usuarios de R. Granada. (http://r-es.org/9jornadasR/)
Romeu Fontanillas, T., Romero Carbonell, M., Guitert Catasús, M. (2016): Technology in Higher Education: 13-20.
Wilcox, R. (2012): Introduction to Robust Estimation & Hypothesis Testing, 3rd edition. Elsevier, Amsterdam, The Netherlands.
Yuen, K.K. (1974): “The Two Sample Trimmed t for Unequal Population Variances”, Biometrika, 61 (1), 165-170.